\({E_i} = \frac{1}{2}{I_1} \times \omega _1^2 + \frac{1}{2}\frac{I}{2} \times \frac{{\omega _1^2}}{4}\)
\( = \frac{{{I_1}\omega _1^2}}{2}\left( {\frac{9}{8}} \right) = \frac{9}{{16}}{I_1}\omega _1^2\)
\({I_1}{\omega _1} + \frac{{{I_1}\omega { _1}}}{4} = \frac{{3{I_1}}}{2}\omega \,\,\,;\,\,\,\frac{5}{4}{I_1}{\omega _1} = \frac{{3{I_1}}}{2}\omega \)
\(\omega = \frac{5}{6}{\omega _1}\,\,\,\,\,\,\,\,\,\,;\,\,\,\,\,\,\,{E_f} = \frac{1}{2} \times \frac{{3{I_1}}}{2} \times \frac{{25}}{{36}}\omega _1^2\)
\( = \frac{{25}}{{48}}{I_1}\omega _1^2\)
\( \Rightarrow {E_f} - {E_i} = {I_1}\omega _1^2\frac{{25}}{{49}} - \frac{{ - 2}}{{48}}{I_2}\omega _1^2\)
\( = \frac{{25}}{{48}}{I_1}\omega _1^2\)
\( \Rightarrow {E_f} - {E_i} = {I_1}\omega _1^2\left( {\frac{{25}}{{48}} - \frac{9}{{16}}} \right) = \frac{{ - 2}}{{48}}{I_1}\omega _1^2\)
\( = \frac{{ - {I_1}\omega _1^2}}{{24}}\)
Download our appand get started for free
Similar Questions
- 1$L $ લંબાઈનો પાતળા સળિયાને એક છેડેથી લટકાવેલો છે અને તે $ n $ ભ્રમણ પ્રતિ સેકન્ડથી ચાકગતિ કરે છે. સળિયાની ચાક ગતિ ઊર્જા કેટલી થશે ?View Solution
- 2નિયમિત ઘનતાનો એક નાનો પદાર્થ પ્રારંભિક વેગ $v$ સાથે વક્ર સપાટી પર ઉપર તરફ ગબડે છે. પદાર્થ તેની પ્રારંભિક સ્થિતિની સાપેક્ષે $3v^2/4g$ મહત્તમ ઊંચાઈ સુધી પહોંચે છે. પદાર્થ કયો હશે?View Solution
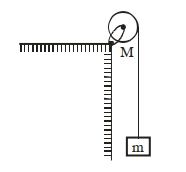
- 3$M=4 \,kg$ દળ અને $R=10 \,cm$ ત્રિજ્યા ધરાવતી એક નિયમિત તક્તિને સમક્ષિતિજ એક્સેલ (ધરી) સાથે આકૃતિમાં દર્શાવ્યા અનુસાર જડવામાં આવેલ છે. $m =2 \,kg$ દળ ધરાવતા ચોસલાને દળરહિત દોરી, કે જેને તક્તિના પરીઘ ઉપર વીંટાળેલ છે, ની મદદથી લટકાવવામાં આવેલ છે. ચોસલાના પતન દરમ્યાન દોરી (તક્તિ ઉપર) સરક્તી નથી અને ધરી માં ધર્ષણ નથી (તેમ ધારો). દોરીમાં તણાવ .............. $N$ હશે. ( $g =10 \,ms ^{-2}$ લો.)View Solution
- 4$a$ બાજુની અને $m$ દળની એક ચોરસ તક્તી વિચારો. આ તક્તીના સમતલને લંબ તથા તેના એક ખૂણામાંથી પસાર થતી અક્ષને અનુલક્ષીને તકતીની જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
- 5એક ઘર્ષણવાળા ટેબલ પર $a$ બાજુ અને $m$ દળ ધરાવતો સમઘન પડેલો છે . સમઘનની કોઈ એક સપાટી પર ટેબલની સપાટી થી $3a\over 4 $ ઊંચાઈએ લંબરૂપે $ F$ બળ લગાવવામાં આવે છે. તો $F$ ના કેટલા ન્યૂનતમ મૂલ્ય માટે બ્લોક સરક્યાં વગર નમશે ?View Solution
- 6View Solutionઢોળાવવાળા સમતલ પર તકતી સરક્યા વિના ગબડે છે. તો તેની કુલ ઊર્જાનો કેટલામો ભાગ ચાકગતિ ઊર્જા સ્વરૂપે મળશે ?
- 7$R$ ત્રિજ્યા અને $9M$ દળની વર્તુળાકાર તકતીમાંથી સમકેન્દ્રિય રહેલ $\frac{R}{3}$ ત્રિજ્યા અને $M$ દળની નાની તકતીને દૂર કરવામાં આવે છે. બાકી રહેલી તકતીની તકતીના સમતલને લંબ અને કેન્દ્રમાંથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
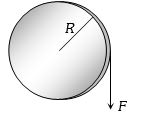
- 8$R$ ત્રિજયા અને $M$ દળ ધરાવતી તકતી તેના કેન્દ્રમાંથી પસાર થતી અને સમતલને લંબ અક્ષને અનુલક્ષીને ચાકગતિ કરી શકે છે.તેના પર સ્પર્શીય બળ $F$ લગાડતાંં સ્પર્શીય પ્રવેગView Solution
- 9જે પદાર્થનો કોણીય વેગમાન $200\%$ વધારવામાં આવે તો તેની ચાકગતિઊર્જામાં ........ $\%$ વધારો થશે.View Solution
- 10$l$ લંબાઈ, $m$ દળવાળો પાતળો સળિયો સમક્ષિતિજ અક્ષને અનુલક્ષીને ઊર્ધ્વસમતલમાં દોલન કરે છે. સળિયાનો મહત્તમ કોણીય વેગ $\omega$ છે, તો તેનું દ્રવ્યમાન-કેન્દ્ર મહત્તમ કેટલી ઊચાઈએ જશે ?View Solution
