બે સમાન વિદ્યુતભાર $x=-a$ અને $x=+a$ $X$- અક્ષ પર મૂકેલાં છે.વિદ્યુતભાર $Q$ ને ઉદ્ગમ બિંદુ પર મૂકેલ છે.હવે,વિદ્યુતભાર $Q$ ને ઘન $X$- દિશા તરફ સૂક્ષ્મ સ્થાનાંતર $x$ કરાવવામાં આવે,તો તેની વિદ્યુતસ્થિતિઊર્જામાં કેટલો ફેરફાર થાય?
IIT 2002, Diffcult
b
(b) Initially according to figure \((i)\) potential energy of \(Q\) is \({U_i} = \frac{{2kqQ}}{a}\) ......\((i)\)
According to figure \((ii)\) when charge \(Q\) is displaced by small distance \(x\) then it’s potential energy now
\({U_f} = kqQ\,\left[ {\frac{1}{{(a + x)}} + \frac{1}{{(a - x)}}} \right]\)\( = \frac{{2kqQa}}{{({a^2} - {x^2})}}\) .......\((ii)\)
Hence change in potential energy
\(\Delta U = {U_f} - {U_i} = 2kqQ\,\left[ {\frac{a}{{{a^2} - {x^2}}} - \frac{1}{a}} \right]\)\( = \frac{{2kqQ{x^2}}}{{({a^2} - {x^2})}}\)
Since \(x << a\) so \(\Delta U = \frac{{2kqQ{x^2}}}{{{a^2}}} \Rightarrow \Delta U \propto {x^2}\)
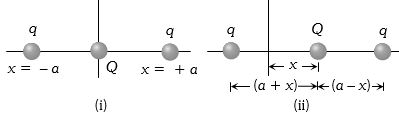
(b) Initially according to figure \((i)\) potential energy of \(Q\) is \({U_i} = \frac{{2kqQ}}{a}\) ......\((i)\)
According to figure \((ii)\) when charge \(Q\) is displaced by small distance \(x\) then it’s potential energy now
\({U_f} = kqQ\,\left[ {\frac{1}{{(a + x)}} + \frac{1}{{(a - x)}}} \right]\)\( = \frac{{2kqQa}}{{({a^2} - {x^2})}}\) .......\((ii)\)
Hence change in potential energy
\(\Delta U = {U_f} - {U_i} = 2kqQ\,\left[ {\frac{a}{{{a^2} - {x^2}}} - \frac{1}{a}} \right]\)\( = \frac{{2kqQ{x^2}}}{{({a^2} - {x^2})}}\)
Since \(x << a\) so \(\Delta U = \frac{{2kqQ{x^2}}}{{{a^2}}} \Rightarrow \Delta U \propto {x^2}\)
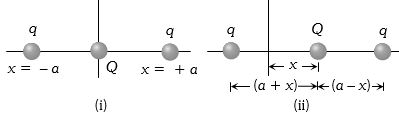
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બે પ્લેટ વચ્ચે $5 \mathrm{~mm}$ અંતર ધરાવતા એક સમાંતર પ્લેટ કેપેસીટરને બેટરી વડે ચાર્જ કરવામાં આવે છે. આ કેપેસીટરની બે પ્લેટ વચચે $2 \mathrm{~mm}$ જાડાઈનો ડાયઈલેક્ટ્રિક સ્લેબ દાખલ કરવામાં આવે ત્યારે કેપેસીટર બેટરી માંથી $25 \%$ જેટલો વધારાનો વિદ્યુતભાર મેળવે છે. તો આ ડાયઈલેકક્ટ્રીક સ્લેબનો ડાયઈલેકિટ્રિક અચળાંક.........View Solution
- 2હવા ધરાવતા સમાંતર પ્લેત કેપેસીટરનો કેપેસીટન્સ $C$ છે. તેને અડધો ડાઈઇલેક્ટ્રિક અચળાંક $5$ થી ભરી દેવામાં આવે તો તેમાં કેપેસીટન્સમાં .....$\%$ નો વધારો થાય?View Solution
- 3View Solutionસમાન ત્રિજયાના ઘન અને પોલા ગોળામાં વિદ્યુતભાર ધારણ કરવાની ક્ષમતા શેમાં વધારે હોય?
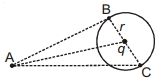
- 4$r$ ત્રિજ્યાવાળા વર્તુળના કેન્દ્ર પર $q$ જેટલો ચાર્જ રાખેલ છે, $B$ અને $C$ બિંદુઓ આ વર્તુંળના પરિઘ પર છે. જ્યારે બિંદુ $A$ આ વર્તુળથી બહાર છે. જો $W_{A B}$ એ $q_0$ ચાર્જને બિંદુ $A$ થી $B$ સુધી લઈ જવા માટેનું કાર્ય દર્શાવે અને $W_{A C}$ એ $q_0$ ચાર્જને બિંદુ $A$ થી $C$ સુધી લઈ જવા માટેનું કાર્ય દર્શાવે તો આપેલી આકૃતિ માટે કયું વિધાન સત્ય છે ?View Solution
- 5$1 \,pF$ કેપેસિટન્સની બે પ્લેટ વચ્ચેનું અંતર બમણું કરીને મીણ ભરી દેતાં નવો કેપેસિટન્સ $2\, pF$ થાય છે.તો મીણનો ડાઇઇલેકિટ્રક અચળાંક કેટલો થાય?View Solution
- 6એક કેપેસિટર પાસે બે વર્તૂળાકાર પ્લેટો છે. જેઓની ત્રિજ્યા $8\,cm$ અને તેની વચ્ચેનું અંતર $1\, mm$ છે. જ્યારે આ પ્લેટોની વચ્ચે મિશ્ર ચોસલુ (ડાઈઈલેકટ્રીક અચળાંક = $6$) મુકવામાં આવે છે. જ્યારે તેને $150\, volt$ સ્થિતિમાન આપવામાં આવે ત્યારે તેમાં સંગ્રહિત ઉર્જાની ગણતરી કરો.View Solution
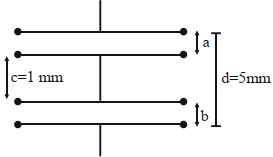
- 7આકૃતિમાં બતાવ્યા પ્રમાણે, $200\,cm ^2$ સમાન પ્લેટનું ક્ષેત્રફળ ધરાવતા બે સમાંતર પ્લેટ કેપેસિટરને એવી રીતે જોડાયેલા છે કે $a \neq b$. સંયોજનનું સમતુલ્ય કેપેસીટન્સ $x \varepsilon_0 F$ છે. $x$ ની કિંમત ................ છે.View Solution
- 8$2 \times 10^{-8}$ કુલમ્બ મીટર જેટલી ડાઈપોલ મોમેન્ટ ધરાવતા ડાઈપોલનાં અક્ષથી $60^{\circ}$ ખુણો અને $3\,m$ નું અંતર ધરાવતાં બિંદુ $\dots\dots$ વિદ્યુત સ્થિતિમાન મળશે.View Solution
- 9$6\ \mu F$ ક્ષમતા વાળા કન્ડેન્સરને $100\, V$ સુધી વિદ્યુતભારીત કરેલ છે તેને બીજા $14\ \mu F$ ક્ષમતા વાળા વિદ્યુતભાર રહીત કન્ડેન્સર સાથે જોડીને છોડી દેવામાં આવે છે. તો $6\ \mu F$ અને $14\ \mu F$ વાળા કન્ડેન્સર પરના વિદ્યુતભારોનો ગુણોત્તર તથા $6\ \mu F$ પરનો વિદ્યુત સ્થીતીમાન.....View Solution
- 10જો $V\,\, = \,\, - 5x\,\, + \,\,3y\,\, + \,\,\sqrt {15} \,z\,$ હોય તો ${\text{E(x, y, z) = }}.....unit$View Solution
