બે વર્તુળાકાર ગૂંચળા $1$ અને $2$ સમાન તારમાંથી બનાવેલ છે પરંતુ પ્રથમ ગૂંચળાની ત્રિજયા બીજા ગૂંચળા કરતાં બમણી છે. તેમની વચ્ચે લગાવવા પડતાં સ્થિતિમાનના તફાવતનો ગુણોત્તર કેટલો હોવો જોઈએ કે જેથી તેમના કેન્દ્ર પર સમાન ચુંબકીયક્ષેત્ર ઉત્પન્ન થાય?
AIPMT 2006, Diffcult
c
Let \(r_{1}\) and \(r_{2}\) are the radius of coil \(1\) and \(2\). If \(B_{1}\) and \(B_{2}\) are magnetic induction at their centre, then
Let \(r_{1}\) and \(r_{2}\) are the radius of coil \(1\) and \(2\). If \(B_{1}\) and \(B_{2}\) are magnetic induction at their centre, then
\(B_{1}=\frac{\mu_{0} I_{1}}{2 r_{1}} ;\) and \(B_{2}=\frac{\mu_{0} I_{2}}{2 r_{2}}\)
Since \(B_{1}=B_{2} ;\) and \(r_{1}=2 r_{2}\)
\(I_{1}=2 I_{2}\)
Again if \(R_{1}\) and \(R_{2}\) are resistance of the coil \(1\) and \(2\) then \(R_{1}=2 R_{2}(\) as \(R \propto\) length \(=2 \pi r)\) and if \(V_{1}\) and \(V_{2}\) are the potential difference across them respectively, then
\(\frac{V_{1}}{V_{2}}=\frac{I_{1} R_{1}}{I_{2} R_{2}}=\frac{\left(2 I_{2}\right)\left(2 R_{2}\right)}{I_{2} R_{2}}=4\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$ 2\pi\, {\rm{ }}cm $ ત્રિજયા ધરાવતી બે સમકેન્દ્રિય રીંગને એકબીજાને લંબ રહે તેમ મૂકેલ છે. તેમાંથી $3A$ અને $4A$ પ્રવાહ પસાર કરતાં કેન્દ્ર પર ચુંબકીયક્ષેત્ર કેટલું થાય?View Solution
- 2બે સમાંતર તાર $A$ અને $B$ માંથી $10\, ampere$ અને $2\, ampere$ નો પ્રવાહ વિરુદ્ધ દિશામાં પસાર થાય છે. તાર $A$ અનંત લંબાઇનો અને તાર $B$ ની લંબાઈ $2\, m$ છે. તાર $A$ થી $10\, cm$ અંતરે રહેલ તાર $B$ પર કેટલું બળ લાગતું હશે?View Solution
- 3હાઇડ્રોજન પરમાણુમાં ઈલેકટ્રોન તેના ન્યુકિલયસને ફરતે $6.76 \times 10^6\,ms ^{-1}$ ઝડપથી $0.52 \mathring A$ ત્રિજ્યાની કક્ષામાં પરિભ્રમણ કરે છે. હાઈડ્રોજન પરમાણુના ન્યુકિલયસમા ઉદભવતું ચુંબકીય ક્ષેત્ર ..... $T$ છે.View Solution
- 4$X-Z$ સમતલમાં ઉગમબિંદુ પર એક એક લંબચોરસ ($5\,cm\times 2\,cm$) $100\,$ આંટાવાળા ગુચળામાથી $3\,A$ પ્રવાહ સમઘડી દિશામાં વહે છે.$X$ અક્ષની દિશામાં $1\,T$ ચુંબકીય ક્ષેત્ર પ્રવર્તે છે.જો ગૂચળાંને $Z$ અક્ષ સાથે $45^o$ના ખૂણે વાળવામાં આવે તો તેના પર કેટલા ......$Nm$ ટોર્ક લાગે?View Solution
- 5બે લાંબા $8\,A$ અને $15\,A$ વીજ પ્રવાહ ધારિત સમાંતર તારને એકબીજાથી $7\,cm$ ના અંતરે રખેલ છે. બંને તારથી સમાન અંતરે બિંદુ $P$ એવી રીતે આવેલું છે કે જેથી બિંદુ $P$ ને તાર સાથે જોડતી રેખાઓ પરસ્પર લંબ થાય. તો $P$ બિંદુુએ ચુંબકીય ક્ષેત્રનું મૂલ્ય $............\times 10^{-6} T$ છે. $\left(\sqrt{2}=1.4\right)$ આપેલું છે.View Solution
- 6$4.0 \mu \mathrm{C}$ નો વિદ્યુતભાર $4.0 \times 10^6 \mathrm{~ms}^{-1}$ ના વેગથી ધન $y$-અક્ષની દિશામાં $(2 \hat{k}) \mathrm{T}$ જેટલી પ્રબળતા ધરાવતા ચુંબકીય ક્ષેત્ર $\vec{B}$ ની અસર હેઠળ ગતિ કરે છે. વિદ્યુતભાર ઉપર લાગતું બળ $x \hat{i} N$ છે.. $x$ નું મૂલ્ય___________છે.View Solution
- 7બે આંટા ધરાવતા વર્તુળાકાર ગાળામાં વહેતા પ્રવાહને કારણે તેના કેન્દ્ર આગળ $B _1$ જેટલું ચુંબકીય પ્રેરણ ઉત્પન્ન થાય છે. આ ગુંચળાને ખોલી તેને ફરી $5$ આંટા ધરાવતા વર્તુળાકાર ગાળા (ગૂંચળા)માં વીટાળવામાં આવે છે અને તેના કેન્દ્ર આગળ સમાન પ્રવાહ માટે $B _2$ જેટલું ચુંબકીય પ્રેરણ ઉત્પન્ન કરે છે. $\frac{B_2}{B_1}$ ગુણોત્તર $........$ થશે.View Solution
- 8અચળ, સમાન અને પરસ્પર લંબ એવાં વિદ્યુતક્ષેત્ર $\overrightarrow{ E }$ અને યુંબકીય ક્ષેત્ $\overrightarrow{ B }$ ના બનેલા પ્રદેશમાં એક વિદ્યુતભારિત કણ $\overrightarrow{v}$ વેગથી $\overrightarrow{ E }$ અને $\overrightarrow{ B }$ બંનેની લંબ દિશામાંથી પ્રવેશે છે અને વેગમાં કોઈપણ પ્રકારના ફેરફાર વિના બહાર આવે છે. કણ પરનો વિદ્યુતભાર $q$ હોય, તો ....View Solution
- 9ચુંબકીય સોયાને ચુંબકીયક્ષેત્રમાં સમતોલન સ્થિતિમાંથી $60^o$ ફેરવવા થતું કાર્ય $W$ છે.તો તેને આ સ્થિતિમાં રાખવા માટે કેટલા ટોર્કની જરૂર પડે?View Solution
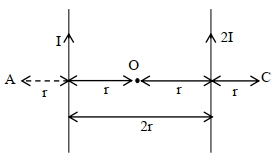
- 10બાજુમાં દર્શાવેલ આકૃતિમાં દર્શાવ્યા અનુસાર બે સમાંતર લાંબા વિદ્યુતપ્રવાહ ધરાવતા તારને $2 r$ અંતરે રાખવામાં આવ્યા છે. બિંદુ $A$ આગળ ચુંબકીય ક્ષેત્ર અને $C$ આગળ ઉત્પન ચુંબકીય ક્ષેત્ર વચ્ચેનો ગુણોતર $\frac{x}{7} $ છે. $x$ નું મૂલ્ચ. . . . . . થશે.View Solution