બહિર્ગોળ લેન્સ દ્વારા રચાતી વાસ્તવિક પ્રતિબિંબ અને પદાર્થ વચ્ચેનું ન્યૂનત્તમ અંતર ......છે.
Easy
b
Let the between object and real image be \(d\).
Let the between object and real image be \(d\).
Let the distance of object from the lens is \(x\)
So the distance of image and lens be \(d - x\)
Using the lens equation :
\(\frac{1}{f}=\frac{1}{v}-\frac{1}{u}\)
\(\frac{1}{f}=\frac{1}{d-x}-\frac{1}{-d}\)
\(x =\frac{ d \pm \sqrt{ d ^2-4 fd }}{2}\)
So for real \(x\)
\(\sqrt{ d ^2-4 fd } \geq 0\)
So \(d \geq 4 f\)
So minimum distance between object and image is \(4 f\).
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક પ્રિઝમ વાદળી અને લાલ કિરણને અનુક્રમે $10^{\circ}$ અને $6^{\circ}$થી વિચલિત કરે છે. અને બીજો પ્રિઝમ $8^{\circ}$ અને $4.5^{\circ}$ થી વિચલિત કરે છે. તો આ બે પ્રિઝમનાં વિભાજન પાવરની સરખામણી કરો.View Solution
- 2$\sqrt 3 $ વક્રીભવનાંકના કાચના લંબચોરસ સ્લેબમાં પ્રકાશનું કિરણ $60° $ આપાત કોણે પ્રવેશે છે. તે સ્લેબમાં $5 \,cm $ અંતર કાપીને સ્લેબની બહાર નિર્ગમન પામે છે. આપાત અને નિર્ગમન કિરણ વચ્ચેનું લંબ અંતર શું થશે?View Solution
- 3એક ટાંકી $12.5\,cm$ ઉંચાઈ સુધી પાણીથી ભરેલી છે. ટાંકીને નીચેની સપાટી પર પડેલી સોયની આભાસી ઉડાઈ માઈક્રોસ્કોપ વડે માપવામાં આવતાં $9.4 \,cm$ મળે છે. તો પાણીનો વક્રીભવનાંક ..... હશે.View Solution
- 4બહિર્ગોળ સપાટી ધરાવતા $1.6$ વક્રીભવનાંકના માધ્યમમાં ધ્રુવથી $12\, cm$ અંતરે બિંદુુગત વસ્તુ છે. વક્રતા ત્રિજ્યા $6 \,cm$ છે. હવામાંથી જોતા પ્રતિબિંબું સ્થાન શોધો.View Solution
- 5દિવાલથી $3 \,m$ અંતરે $3\, cm$ ઊંચાઇની મીણબત્તી મૂકેલી છે,દિવાલથી કેટલા......$cm$ અંતરે અંર્તગોળ અરીસો મૂકવાથી દિવાલ પર $9 \,cm$ ઊંચાઇનું પ્રતિબિંબ મળે?View Solution
- 6$20\, cm$ કેન્દ્રલંબાઈ ધરાવતો બહિર્ગોળ લેન્સ $'A'$ અને $5\, cm$ કેન્દ્રલંબાઈ ધરાવતા અંતર્ગોળ લેન્સ $'B'$ ને તેમની વચ્ચે $'d'$ જેટલું અંતર રહે તેમ સમાન અક્ષ પર મૂકવામાં આવે છે. જે $'A'$ પર આપાત સમાંતર પ્રકાશ કિરણપૂંજ $'B'$ માંથી સમાંતર કિરણપૂંજ તરીકે નિર્ગમન પામતું હોય, તો અંતર $'d'$ $......\,cm$ હશે.View Solution
- 7View Solutionબે સમાન સમતલ બર્હિગોળ લેન્સને આકૃતિ મુજબ મૂકતાં તેમની કેન્દ્રલંબાઇનો ગુણોત્તર કેટલો થાય?
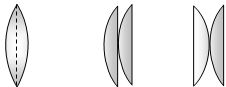
- 8View Solutionહીરો ચળકતો દેળાય છે.કારણ કે...
- 9પ્રિઝમમાંથી પીળો પ્રકાશ લઘુતમ વિચલન સાથે વક્રીભૂત થાય છે. જો $i_1$ અને $i_2$ પ્રિઝમ માટે આપાતકોણ અને નિર્ગમનકોણ હોય, તોView Solution
- 10$40cm$ વક્રતાત્રિજયા ધરાવતા અંર્તગોળ અરીસા દ્વારા પ્રતિબિંબની ઊંચાઇ વસ્તુ કરતાં બમણી મેળવવા માટે,વસ્તુ અંતર કેટલા ......$cm$ હોવું જોઈએ?View Solution
