Moment of the force is,
\(\begin{array}{l}
\overrightarrow \tau = \left( {\overrightarrow r - \overrightarrow {{r_0}} } \right) \times \overrightarrow F \\
Here,\,\overrightarrow {{r_0}} = 2\hat i - 2\hat j - 2\hat k\\
and\,\,\overrightarrow r = 2\hat i + 0\hat j - 3\hat k\\
\therefore \,\overrightarrow r - \overrightarrow {{r_0}} = \left( {2\hat i + 0\hat j - 3\hat k} \right) - \left( {2\hat i - 2\hat j - 2\hat k} \right)\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 0\hat i + 2\hat j - \hat k\\
\therefore \,\,\,\overrightarrow \tau \, = \left| \begin{array}{l}
\hat i\,\,\,\,\,\,\hat j\,\,\,\,\,\,\,\,\hat k\\
0\,\,\,\,\,\,2\,\,\,\,\, - 1\\
4\,\,\,\,\,\,5\,\,\,\, - 6
\end{array} \right| = - 7\hat i - 4\hat j - 8\hat k
\end{array}\)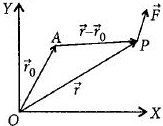
Download our appand get started for free
Similar Questions
- 1નકકર ગોળો વ્યાસને અનુલક્ષીને ફરે છે. તાપમાન વઘવાથી તેના કદમાં $1\%$ નો વઘારો થાય છે. તો કોણીય ઝડપView Solution
- 2$\vec r$ સ્થાનસદિશ ઘરાવતા કણ પર લાગતું બળ $\vec F$ છે.આ બળથી ઉગમબિંદુની સાપેક્ષે લાગતું ટોર્ક $\vec \tau $ છે, તો..........View Solution
- 3$R$ ત્રિજયાવાળો ઘન ગોળો ધર્ષણરહિત સમક્ષિતિજ સપાટી પર પડેલ છે. $F$ સમક્ષિતિજ બળ નીચેના બિંદુથી $h$ ઊંચાઇ પર લગાવતા દ્રવ્યમાનકેન્દ્રનો મહત્તમ પ્રવેગ મેળવવા માટે નીચે પૈકી શું સાચું થાય?View Solution
- 4$3\; m$ લંબાઈના સળિયાનું એકમ લંબાઈ દીઠ દળ એ તેના એક છેડાથી અંતર $x$ ના સમપ્રમાણમાં બદલાય છે, તો આ સળિયાનું દ્રવ્યમાનકેન્દ્ર તેના એક છેડેથી કેટલા અંતરે ($m$ માં) હશે?View Solution
- 5એક મીટર સ્ટીકનો તેનાં એક છેડો તળીયા પર રહે તેમ શિરોલંબ રીતે મૂકવામાં આવે છે અને તેને છોડવામાં આવે છે, જ્યારે તેનો બીજો છેડો તળીયા સાથે અથડાય ત્યારે તેની ઝડપ ............... $m / s$ (ધારો કે તળીયા પર રહેલો છેડો લપસી જતો નથી.) $\left(g=9.8 \,m / s ^2\right)$View Solution
- 6નીચેનામાંથી કયાં વિધાનો સાચા છે?View Solution
$(a)$ પદાર્થનું દ્રવ્યમાનકેન્દ્ર અને ગુરુત્વાકર્ષણનું કેન્દ્ર હંમેશા સંપાત થાય.
$(b)$ પદાર્થનું દ્રવ્યમાનકેન્દ્ર એ બિંદુએ હોય જ્યાં પદાર્થ પર લાગતું કુલ ગુરુત્વાકર્ષી ટોર્ક શૂન્ય હોય.
$(c)$ બળયુગ્મ પદાર્થમાં રેખીય અને ચાક બંને ગતિ ઉત્પન્ન કરે
$(d)$ યાંત્રિક લાભનું મૂલ્ય એક $1$ કરતા વધારે હોવાનો અર્થ એ છે કે ઓછા પ્રયત્નથી વધુ ભાર ઉપાડી શકાય.
- 7એક $M$ દળ અને $R$ ત્રિજ્યા ધરાવતી તકતીનું એકમ ક્ષેત્રફળ દીઠ દળ $\sigma (r) = kr^2$ મુજબ આપવામાં આવે છે જ્યાં $r$ એ તકતીના કેન્દ્રથી અંતર છે.તો તેના સમતલને લંબ અને દ્રવ્યમાન કેન્દ્રમાથી પસાર થતી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
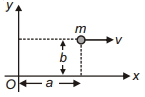
- 8નીચે દર્શાવ્યા પ્રમાણે $x$ અક્ષને સમાંતર $v$ જેટલાં અચળ વેગ સાથે એક $m$ દળનો કણ ગતિ કરી રહ્યો છે. $O$ ઉગમબિંદુને અનુલક્ષીને તેનો કોણીય વેગમાન શું થાય?View Solution
- 9$M$ દળની વર્તૂળાકાર તકતીનો પ્રારંભિક વેગ $\omega_1$ છે. બે નાના $ m $ દળના ગોળાઓને તકતીના વ્યાસના વિરૂદ્ધ બિંદુઓ પર જોડેલા છે. તકતીનો અંતિમ કોણીય વેગ શું થશે ?View Solution
- 10સમાન દળ અને ત્રિજ્યા $R$ ધરાવતી બે રીંગો ને તેમના એેક બીજા થી લંબ સમતલો સાથે અને તેમનું કેન્દ્ર એક સહિયારા બિંદુુ પર રહે તેમ મૂકવામાં આવે છે. એક રીગના સમતલને લંબ અને તેના કેન્દ્રમાંથી પસાર થતી અક્ષને અનુલક્ષીને ચક્રાવર્તન ત્રિજ્યા શું હશે?View Solution
