(બળના $SI$ એકમ) $1$ newton ને (બળના $CGS$ એકમ) ડાઈનમાં રૂપાંતરણ કરતા...... મળેે.
Easy
Download our app for free and get started
d
બળનું પારિમાણિક સૂત્ર $ [F] = [M^1L^1T^{-2}]$
બળનું પારિમાણિક સૂત્ર $ [F] = [M^1L^1T^{-2}]$
તેથી જો $ n_1, u_1, $ અને $n_2, u_2$ એ અનુક્રમે $SI $ અને $CGS $ એકમ છો. તો,
$\,{{\rm{n}}_{\rm{1}}}\,\,{\left[ {\frac{{{{\rm{M}}_{\rm{1}}}}}{{{{\rm{M}}_{\rm{2}}}}}} \right]^{\rm{1}}}{\rm{ }}\,{\left[ {\frac{{{{\rm{L}}_{\rm{1}}}}}{{{{\rm{L}}_{\rm{2}}}}}} \right]^1}\,\,{\left[ {\frac{{{T_1}}}{{{T_2}}}} \right]^{{\rm{ - 2}}}}$
$ = \,\,{\rm{1}}\,\,\left[ {\frac{{{\rm{kg}}}}{{\rm{g}}}} \right]\,\,\left[ {\frac{{\rm{m}}}{{{\rm{cm}}}}} \right]\,\,{\left[ {\frac{{\rm{s}}}{{\rm{s}}}} \right]^{{\rm{ - 2}}}}$
$ = \,\,{\rm{1}}\,\, \times \,\,{\rm{1000}}\,\, \times \,\,{\rm{100}}\,\, \times \,\,{\rm{1}}{{\rm{0}}^{\rm{5}}}\,$
$1$ ન્યુટન = $1{0^5}$ ડાઈન
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1જો એક અવરોધનું મૂલ્ય $10.845 \,\Omega$ હોય અને પસાર થતા વિદ્યુતપ્રવાહનું મૂલ્ય $3.23 \,A$ છે, તો સાર્થક અંકોની સાથે વિજસ્થિતમાનના તફાવત નું મુલ્ય .............. વોલ્ટ થાય ?View Solution
- 2રિંગના દળ, ત્રિજ્યા અને કોણીય વેગના માપનમાં મહત્તમ પ્રતિશત ક્ષતિ અનુક્રમે $ 2\%, 1\% $ અને $1\%$ છે તો ભૌગોલિક અક્ષ $J$ નું કોણીય વેગમાન $ I \omega $ ની મહત્તમ પ્રતિશત ક્ષતિ ........ $\%$ હશે.View Solution
- 3સૂચિ $I$ અને સૂયિ $II$ મેળવોView Solution
List $I$ List $II$ $A$ ટોર્ક $I$ ${\left[\mathrm{M}^1 \mathrm{~L}^1 \mathrm{~T}^{-2} \mathrm{~A}^{-2}\right]}$ $B$ ચુંબકીય ક્ષેત્ર $II$ $\left[\mathrm{L}^2 \mathrm{~A}^1\right]$ $C$ ચુંબકીય ચાક્માત્રા $III$ ${\left[\mathrm{M}^1 \mathrm{~T}^{-2} \mathrm{~A}^{-1}\right]}$ $D$ મુક્ત અવકાશની પારગામયતા $IV$ $\left[\mathrm{M}^1 \mathrm{~L}^2 \mathrm{~T}^{-2}\right]$ નીચે આપેલા વિકલ્પોમાંથી સાચો ઉત્તર પસંદ કરોઃ
- 4View Solutionકોણીય વેગમાનનો એકમ શું થાય?
- 5કણનો વેગ $ v = a + bt + c{t^2} $ હોય,તો $a$ નો એકમ શું થાય?View Solution
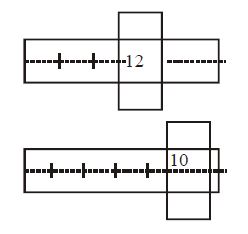
- 6એક સ્ક્રૂ ગેજમાં અમુક ત્રુટિ છે જેનું મૂલ્ય અજ્ઞાત છે. આપની પાસે બે સમાન સળિયા છે. જ્યારે પહેલા સળિયાને સ્ક્રૂ ગેજમાં દાખલ કરવામાં આવે ત્યારે આકૃતિ $(I)$ પ્રમાણે દેખાય છે. જ્યારે બંને સળિયાને સાથે શ્રેણીમાં જોડીને સ્ક્રૂ ગેજમાં દાખલ કરવામાં આવે ત્યારે આકૃતિ $(II)$ પ્રમાણે દેખાય છે. તો સાધનની શૂન્ય ત્રુટિ કેટલા $mm$ હશે?View Solution
$1\,M.S.D. = 100\, C.S.D. = 1\, mm $
- 7View Solutionલેન્સના કેન્દ્રીય પાવરનું પરિમાણ શું છે?
- 8View Solutionનીચેના માથી સરખા પરિમાણ વાળુ જોડકુ પસંદ કરો.
- 9ટ્રાવેલીગ માઈક્રોસ્કોપની મદદથી કાચના ચોસલા (slab) નો વકીભભવનાંક શોધવા માદે નીચે મુજબના અવલોકનો મળે છે. $50$ વર્નિયર સ્કેલના વિભાગ$=49\ MSD$ (મુખ્ય સ્કેલના વિભાગો) દરેક $cm$ ની લંબાઈમાં મુખ્ય સ્કેલ ઉપર $20$ વિભાગો છે. પેપર પરના માર્ક (નિશાની) માટેનું અવલોકનView Solution
$\text { M.S.R }=8.45 \mathrm{~cm}, V.C =26$
ચોસલામાંથી જોતાં પેપર પરના માર્ક (નિશાની) માટેનું અવોલક્ન$\text { M.S.R }=7.12 \mathrm{~cm}, V . C=41$
કાચની સપાટી ઉપરના પાવડર કણો માટેનું અવલોકન$\text { M.S.R }=4.05 \mathrm{~cm}, \mathrm{~V} . \mathrm{C}=1$
કાચના ચોસલાનો વક્કીભવનાંક. . . . .થશે.($M.S.R$. = મુખ્ય સ્કેલ પરનું અવલોકન$V.C$. = વર્નિંયર કેલીપર્સના કાપા)
- 10જો $A$ અને $B$ ના પરિમાણિક સૂત્ર સમાન ના હોય તો નીચેનમનથી કઈ વસ્તુ શક્ય નથી?View Solution