જો $A$ અને $B$ ના પરિમાણિક સૂત્ર સમાન ના હોય તો નીચેનમનથી કઈ વસ્તુ શક્ય નથી?
Easy
Download our app for free and get started
a
\(A -B\) can not be possible in any case if \(A\) and \(B\) have unequal dimensions.
\(A -B\) can not be possible in any case if \(A\) and \(B\) have unequal dimensions.
\(\therefore\) Ans \(\perp\) is correct
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પ્રકાશની તરંગલંબાઇ $ 0.00006\,m $ હોય,તો માઇક્રોમાં તેનું મુલ્ય .......... $microns$ થશે.View Solution
- 2ઓહમના નિયમના પ્રયોગમાં જુદાં જુદાં અવલોકનો દરમિયાન એક અજ્ઞાત અવરોધનું મૂલ્ય $4.12 \Omega , 4.08 \Omega , 4.22 \Omega $ અને $ 4.14 \Omega$ મળે છે. અવલોકનમાં નિરપેક્ષ ત્રુટિ અને સાપેક્ષ ત્રુટિ અનુક્રમે ....... મળે.View Solution
- 3એક અલગ કરેલા તંત્રમાં વાયુ અણુઓ દ્વારા થતું કાર્ય $W =\alpha \beta^{2} e ^{-\frac{ x ^{2}}{\alpha kT }},$, જ્યાં $x$ એ સ્થાનાંતર, $k$ બોલ્ટ્ઝમેન અચળાંક અને $T$ તાપમાન છે. $\alpha$ અને $\beta$ અચળાંક છે. $\beta$ નું પરિમાણ .........View Solution
- 4એક સ્ક્રુગેજમાં, વર્તુળાકાર સ્કેલ પર $100$ કાપાઓ છે અને વર્તુળાકાર સ્કેલના એક પૂર્ણ પરિભ્રમણ માટે મુખ્ય સ્કેલ $0.5\,mm$ અંતર કાપે છે. વર્તુળાકાર સ્કેલ પરનો શૂન્યનો કાપો જયારે બંને જડબાને એકબીજા સાથે જોડવામાં આવે છે ત્યારે, સંદર્ભ રેખાથી $6$ કાપાની નીચે રહે છે. જયારે તારને જડબાની વચ્ચે રાખવામાં આવે છે ત્યારે $4$ રેખીય કાપાઓ સ્પષ્ટતાથી જોઈ શકાય છે જયારે વર્તુળાકાર સ્કેલ પરનો $46$ મો કાપો સંદર્ભ રેખા સાથે સંપાત થાય છે. તારનો વ્યાસ $..........\times 10^{-2}\,mm$ થશે.View Solution
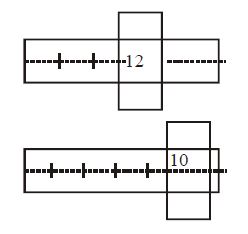
- 5એક સ્ક્રૂ ગેજમાં અમુક ત્રુટિ છે જેનું મૂલ્ય અજ્ઞાત છે. આપની પાસે બે સમાન સળિયા છે. જ્યારે પહેલા સળિયાને સ્ક્રૂ ગેજમાં દાખલ કરવામાં આવે ત્યારે આકૃતિ $(I)$ પ્રમાણે દેખાય છે. જ્યારે બંને સળિયાને સાથે શ્રેણીમાં જોડીને સ્ક્રૂ ગેજમાં દાખલ કરવામાં આવે ત્યારે આકૃતિ $(II)$ પ્રમાણે દેખાય છે. તો સાધનની શૂન્ય ત્રુટિ કેટલા $mm$ હશે?View Solution
$1\,M.S.D. = 100\, C.S.D. = 1\, mm $
- 6View Solutionનીચેનામાંથી કયા સંબંધની મદદથી પરિમાણનું પૃથ્થકરણ કરી શકાય છે?
- 7એક તારનો વ્યાસ માપવા વપરાતા એક સ્ક્રુ ગેજ નીચે પ્રમાણેનાં અવલોકનો દર્શાવે છેView Solution
મુખ્ય માપનું અવલોકન: $0\;mm$
વર્તુળાકાર માપનું અવલોકન: $52$ મો કાપો મુખ્ય માપ પરનો $1\;mm$ વર્તૂળાકારનાં $100$ કાપા બરાબર છે તેમ આપેલું છે. ઉપરોક્ત માહિતી પરથી તારનો વ્યાસ કેટલો થાય?
- 8પેકેટમાં $20.23 \,g \pm 0.01 \,g$ નો ચાંદીનો પાવડર છે. $5.75 \,g \pm 0.01 \,g$ દળનો કેટલો પાવડર તેમાંથી લેવામાં આવે છે. બાકી બચેલા પાવડરનું દળ .......... હશે?View Solution
- 9$l,r,c$ અને $v$ અનુક્રમે પ્રેરકત્વ, અવરોધ, સંગ્રાહકતા (કેપેસિટન્સ) અને વોલ્ટેજ રજૂ કરે છે. $\frac{l}{rcv}$ નો $SI$ એકમ પધ્ધતીમાં પરિમાણ કેટલું થશે?View Solution
- 10કોઇ પદ્ધતિ માં પ્રકાશનો વેગ $(c)$, ગુરુત્વાકર્ષણ અચળાંક $(G)$ અને પ્લાન્ક અચળાંક $(h)$ ને મૂળભૂત એકમો તરીકે લીધેલા છે. તો આ નવી પદ્ધતિ મુજબ જડત્વની ચાકમાત્રાનું પરિમાણિક સૂત્ર શુ થાય?View Solution