બંધ પાઇપમાં સ્થિત તરંગ $ y = 2a\sin kx\cos \omega \,t $ હોય,તો તે $ y = a\sin (\omega \,t - kx) $ અને કયાં તરંગના સંપાતીકરણના કારણે મળે ?
Easy
Download our app for free and get started
b
(b) In closed organ pipe.
(b) In closed organ pipe.
If \({y_{incident}} = a\sin (\omega t - kx)\)
then \({y_{reflected}} = a\sin (\omega t + kx + \pi ) = - a\sin (\omega t + kx)\)
Superimposition of these two waves give the required stationary wave.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1તરંગનું સમીકરણ $y = {10^4}\sin (60t + 2x).$ જ્યાં $x$ અને $y$ એ મીટર અને $t$ એ સેકન્ડમાં છે.View Solution
- 2View Solutionનીચેનામાંથી કયું વિધાન સાચું છે.
- 3બે ટ્રેન એકબીજા તરફ સમાન ઝડપથી ગતિ કરે છે. ધ્વનિની ઝડપ $340 m / s$ છે. જો એક ટ્રેનના હોર્નની આવૃતિ બીજી ટ્રેનના ડ્રાઇવરને $9/8$ ગણી સંભળાતી હોય, તો દરેક ટ્રેનની ઝડપ ($m/s$ માં) કેટલી હશે?View Solution
- 4તારનો પ્રથમ ઓવરટોન $320Hz$, હોય તો મૂળભૂત આવૃત્તિ કેટલી .... $Hz$ થાય?View Solution
- 5જો ઓકિસજનની ઘનતા હાઇડ્રોજન કરતાં $16$ ગણી હોય,તો ધ્વનિની ઝડપનો ગુણોત્તર કેટલો થાય?View Solution
- 6એક બાઇક પાછળ પોલિસની કાર $22 m/s$ ની ઝડપથી જઇ રહી છે.પોલીસની કાર દ્રારા $176 Hz $ આવૃતિ ઘરાવતો હોર્ન વગાડવામાં આવે છે. બંને એક $165 Hz$ ઘરાવતા સાઇરન તરફ ગતિ કરી રહયા છે.જો બાઇક સવારને સ્પંદ અનુભવાતા ન હોય તો બાઇકની ઝડપ ... $m/s$ કેટલી હશે? (હવામાં ઘ્વનિની ઝડપ $330 m/s$ )View Solution
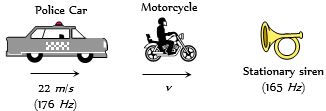
- 7$51.6 \;cm $ અને $49.1 \;cm$ લંબાઇ ધરાવતા બે તારના છેડે અલગથી $20\; N$ જેટલું બળ લગાડેલ છે. બંને તારનું એકમ લંબાઇ દીઠ દળ સમાન અને $1\; g/m $ ને બરાબર છે. જ્યારે બંને તારને એકસ્થે કંપન કરાવવામાં આવે, તો સ્પંદની સંખ્યા કેટલી હશે?View Solution
- 8હવાના કણોનું સ્થાનાંતર $(s)$ એ ધ્વનિના તરંગ દ્વારા ઉત્પન્ન થતાં દબાણના તફાવત $(\Delta p)$ ના સમપ્રમાણમાં છે. સ્થાનાંતર $(s)$ એ ધ્વનિની ઝડપ $(v),$ હવાની ઘનતા $(\rho)$ અને આવૃતિ $(f)$ પર પણ આધાર રાખે છે. જો $\Delta p \approx 10\, Pa , v \approx 300\, m / s , p \approx 1\, kg / m ^{3}$ અને $f \approx 1000 \,Hz$ હોય તો $s$ નું મૂલ્ય કયા ક્રમનું હશે?View Solution
(ગુણકારનો અચળાંક $1$ લો)
- 9સાઇનોસાઇડલ તરંગ $y = 0.40\cos [2000\,t + 0.80\,x]\,m$ ની આવૃત્તિ કેટલી થાય?View Solution
- 10એક અનુનાદ નળીમાં બે અનુક્રમિત જગ્યાઓના સ્થાન $15 \,cm$ અને $48 \,cm$ અંતરે છે. જો સ્વરકાંટાની આવૃતિ $500 \,cps$ હોય તો અવાજની ઝડપ ........... $m/s$ હોય.View Solution