બુલેટ એક પાટિયામાથી પસાર થઈ ને તેના વેગનો ${\left( {\frac{1}{n}} \right)^{th}}$ મો વેગ ગૂમાવે છે. તો બુલેટ ને સ્થિર કરવા માટે આવા કેટલા પાટિયા જોઈએ?
JEE MAIN 2014, Diffcult
a
\(\begin{array}{l}
\left( a \right)\,\,\,\,\,\,Let\,u\,be\,the\,initial\,velocity\,of\,the\,bullet\,of\,\\
\,\,\,\,\,\,\,\,\,\,\,\,mass\,m.\\
\,\,\,\,\,\,\,\,\,\,\,\,After{\rm{ passing}}\,through\,a\,plank\,of\,width\,x,\\
\,\,\,\,\,\,\,\,\,\,\,\,its\,velocity\,decreases\,to\,v.\\
\,\,\,\,\,\,\,\,\,\,\,\,\therefore \,u - v = \frac{4}{n}\,{\kern 1pt} or,\,v = u - \frac{4}{n} = \frac{{u\left( {n - 1} \right)}}{n}\\
\,\,\,\,\,\,\,\,\,\,\,\,\,IfF\,be\,the\,retarding\,force\,applied\,d\,by\,each\,\\
\,\,\,\,\,\,\,\,\,\,\,\,\,plank,\,then\,{\rm{ using}}\,work\, - \,energy\,theorem,\\
Fx = \frac{1}{2}m{u^2} - \frac{1}{2}m{v^2} = \frac{1}{2}m{u^2} - \frac{1}{2}m{u^2}\frac{{\left( {n - {1^2}} \right)}}{{{n^2}}}\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{2}m{u^2}\left[ {\frac{{1 - \left( {n - {1^2}} \right)}}{{{n^2}}}} \right]
\end{array}\)
\(\begin{array}{l}
\left( a \right)\,\,\,\,\,\,Let\,u\,be\,the\,initial\,velocity\,of\,the\,bullet\,of\,\\
\,\,\,\,\,\,\,\,\,\,\,\,mass\,m.\\
\,\,\,\,\,\,\,\,\,\,\,\,After{\rm{ passing}}\,through\,a\,plank\,of\,width\,x,\\
\,\,\,\,\,\,\,\,\,\,\,\,its\,velocity\,decreases\,to\,v.\\
\,\,\,\,\,\,\,\,\,\,\,\,\therefore \,u - v = \frac{4}{n}\,{\kern 1pt} or,\,v = u - \frac{4}{n} = \frac{{u\left( {n - 1} \right)}}{n}\\
\,\,\,\,\,\,\,\,\,\,\,\,\,IfF\,be\,the\,retarding\,force\,applied\,d\,by\,each\,\\
\,\,\,\,\,\,\,\,\,\,\,\,\,plank,\,then\,{\rm{ using}}\,work\, - \,energy\,theorem,\\
Fx = \frac{1}{2}m{u^2} - \frac{1}{2}m{v^2} = \frac{1}{2}m{u^2} - \frac{1}{2}m{u^2}\frac{{\left( {n - {1^2}} \right)}}{{{n^2}}}\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{1}{2}m{u^2}\left[ {\frac{{1 - \left( {n - {1^2}} \right)}}{{{n^2}}}} \right]
\end{array}\)
\(\begin{array}{l}
Fx = \frac{1}{2}m{u^2}\left( {\frac{{2n - 1}}{{{n^2}}}} \right)\\
Let\,P\,be\,the\,number\,of\,planks\,required\,to\,\\
stope\,the\,bullet.\\
Total\,{\rm{distance}}\,travelled\,by\,the\,bullet\,be\,fore\\
{\rm{ coming}}\,torest = Px\\
{\rm{Using}}\,{\rm{work - energy}}\,{\rm{theorem}}\,{\rm{aging,}}\\
F\left( {Px} \right) = \frac{1}{2}m{u^2} - 0\\
or,\,P\left( {Fx} \right) = P\left[ {\frac{1}{2}m{u^2}\frac{{\left( {2n - 1} \right)}}{{{n^2}}}} \right] = \frac{1}{2}m{u^2}\\
\therefore \,P = \,\frac{{{n^2}}}{{2n - 1}}\,
\end{array}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક પાણીના પંપની પાવર $4 \,kW$ છે. જો $g=10 \,ms ^{-2}$, તો તે $1$ મિનીટ માં. $20 \,m$ ઊંચાઈ પર પાણીનાં જથ્થોને માત્રા ને .............. લીટર લઈ જઈ શકેView Solution
- 2$5\, kg$ ના બ્લોક અને સપાટી વચ્ચેનો ઘર્ષણાંક $0.2$ છે,તેના પર $25 \,N $ નું બળ દ્વારા $10 \,m$ ખસેડતાં બ્લોક ........ $J$ ગતિઉર્જા પ્રાપ્ત કરશે.View Solution
- 3વિધાન: $m$ દળના નાના $n$ દડાઓ $u$ વેગથી દર સેકંડે સપાટી સાથે સ્થિતિસ્થાપક સંઘાત રચે છે. સપાટી દ્વારા અનુભવાતું બળ $2\,mnu$ હશે.View Solution
કારણ: સ્થિતિસ્થાપક સંઘાત બાદ દડો તેટલા જ વેગ થી ઉછળે છે.
- 4કણ પર બળ $\vec F = 10\hat i + 10\hat j + 20\hat k\,N.$લાગતા તેનો વેગ $\vec v = 5\hat i - 3\hat j + 6\hat k\,m{s^{ - 1}}$હોય,તો પાવર.......$J-s^{-1}$View Solution
- 5$F=\left(5+3 y^2\right)$ જેટલું બળ કણ ઉપર $y-$દિશામાં પ્રવર્તે છે, જ્યાં $F$ એ ન્યૂટનમાં અને $y$ એ મીટરમાં છે. $y=2\,m$ થી $y=5\,m$ સુધીના સ્થાનાંતર દરમિયાન બળ દ્વારા થતું કાર્ય $...........\,J$ થશે.View Solution
- 6બે ગાડીઓ વચ્ચે મૂકેલાં વિજભારના વિસ્ફોટ થવાથી બંને ગાડાઓ એકબીજાથી દૂર ધકેલાય છે. $100 kg $ વજનનું ગાડું $18 $ મીટર અંતર કાપીને અટકી જાય છે. $300 kg $ વજનનું ગાડું કેટલા .......$m$ અંતર કાપીને અટકતું હશે? જમીન સાથે ગાંડાઓનો ઘર્ષણ અચળાંક $\mu$ સમાન છે.View Solution
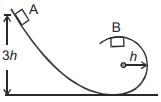
- 7આકૃતિ માં દર્શાવ્યા મુજબ, એક પદાર્થને લીસા ટ્રેક ઉપર $A$ સ્થાને થી છોડવામાં આવે છે. જ્યારે પદાર્થ $B$ પર પહોંચે છે, ત્યારે ટ્રેક વડે તેના પર લાગેલ લંબપ્રતિક્રિયા બળ ....... છે?View Solution
- 8એક લાંબી સ્પ્રિંગને $2\,cm$ ખેંચવામાં આવે ત્યારે તેની સ્થિતિ ઊર્જા $U$ છે.જો સ્પ્રિંગને $8\,cm$ ખેંચવામાં આવે તો તેમાં સંગ્રહ થતી સ્થિતિ ઊર્જા $..........\,U$ થશે.View Solution
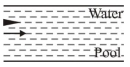
- 9આકૃતિમાં દર્શાવ્યા મુજબ, $200\,g$ દળ ધરાવતી બુલેટ (ગોળી)ને $90\,J$ જેટલી પ્રારંભિક ગતિઉર્જા સાથે એક લાંબા સ્નાનાગારમાં ફાયર(છોડવામાં) આવે છે. જો તેની ગતિઉર્જા $1\,s$ માં ધટીને $40\,J$ થાય, તો બુલેટ સંપૂર્ણ રીતે વિરામ સ્થિતમાં આવે તે માટે ગોળી એ સ્નાનાગારમાં કાપવું પડતું લધુત્તમ અંતર $.......\,m$ હશે.View Solution
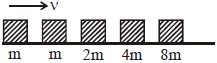
- 10$m , 2 m , 4 m$ અને $8 m$ દળના બ્લોકને ઘર્ષણરહિત સપાટી પર મુકેલ છે.આકૃતિમાં દર્શાવ્યા પ્રમાણે બીજો $m$ દળનો બ્લોક તે જ રેખા પર $v$ વેગથી ગતિ કરીને $m$ દળના બ્લોક સાથે સંપૂર્ણ અસ્થિતિસ્થાપક સંઘાત અનુભવે છે. બિજા બધા પછીના સંઘાત સંપૂર્ણ અસ્થિતિસ્થાપક સંઘાત છે. જે સમયે $8m$ દળનો બ્લોક ગતિ કરવાનું શરૂ કરે ત્યારે તેની શરૂઆતની કુલ ઉર્જા ની $p \%$ ઉર્જાનો વ્યય થાય છે. તો $p$ નું મૂલ્ય લગભગ કેટલું હશે?View Solution