ચાર અવરોધો $15\; \Omega, 12\; \Omega, 4 \;\Omega$ અને $10\; \Omega$ ને વર્તુળાકાર વ્હીસ્ટન બ્રિજ પરિપથની જેમ જોડેલા છે.તો પરિપથને સમતોલિત કરવા માટે $10\; \Omega$ અવરોધ સાથે કેટલાનો ............... અવરોધ($\Omega$ માં) સમાંતરમાં જોડાવો પડે?
JEE MAIN 2020, Medium
b
Let the resistance to be connected is \(\mathrm{R}\). For balanced wheatstone bridge.
Let the resistance to be connected is \(\mathrm{R}\). For balanced wheatstone bridge.
\(15 \times 4=12 \times \frac{10 \mathrm{R}}{10+\mathrm{R}}\)
\(\Rightarrow \mathrm{R}=10 \Omega\)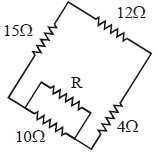
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1પોટેન્શિયોમિટર તારની લંબાઇ $100\,cm$ છે અને સ્ટાન્ડર્ડ બેટરીનું $emf \, E \,volt$ છે.તેનો ઉપયોગ $0.5Ω$ આંતરિક અવરોધ ધરાવતી બેટરીનું $emf$ શોધવા માટે કરવામાં આવેલ છે.જો તટસ્થ બિંદુ ધન છેડાથી $l=30 \,cm$ અંતરે મળતું હોય,તો બેટરીનું $emf=$ કેટલો હશે?View Solution
જયાં $i$ એ પોટેન્શિયોમિટર તારનો પ્રવાહ છે.
- 2કોપરની પટ્ટી અને જર્મેનિયમની પટ્ટીને રૂમ તાપમાનથી $80\, K$ તાપમાન સુધી ઠંડી પાડવામાં આવે તો તેમના અવરોધ વિષે શું કહી શકાય?View Solution
- 3$0.5\, mm$ ત્રિજ્યા ધરાવતાં અને $5 \times 10^{7}\, S / m$ જેટલી વાહકતા ધરાવતાં એક નળાકારીય તારને લગાડેલા $10\, mV/m$ જેટલા વિદ્યુતક્ષેત્રમાં દાખલ કરવામાં આવે છે. તારમાં વહેતા પ્રવાહનું અપેક્ષિત મૂલ્ય $x ^{3} \,\pi mA$ છે. $x$ નું મૂલ્ય ...... .View Solution
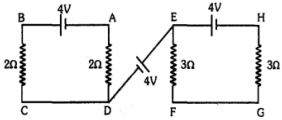
- 4ત્રણ સમાન બેટરીનું $emf\ 4\ V$ અને અવગણ્ય આંતરીક અવરોધ શૂન્ય છે. જેમનું જોડાણ આકૃતિમાં બતાવ્યું છે. બિંદુઓ $A$ અને $G\ (V_A - V_G)$ વચ્ચેનો સ્થિતિમાનનો તફાવત ................ $V$ છે.View Solution
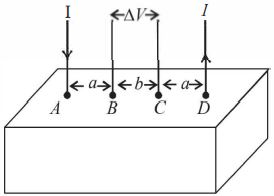
- 5આકૃતિમાં દર્શાવ્યા પ્રમાણેનાં $\rho $ અવરોધકતાનાં વાહક દ્રવ્યને એક ચોસલો ધારો. વિદ્યુત પ્રવાહ $I, A$ આગળ દાખલ થાય છે $D$ આગળથી છોડે (બહાર નીકળે) છે. $B$ અને $C$ વચ્ચે ઉદભવતાં વોલ્ટેજ $\Delta V$ શોધવા સંપાતપણા સિદ્ધાંત લાગુ પાડવામાં આવે છે. નીચેના ક્રમમાં ગણત્રી કરવામાં આવે છે.View Solution
$[A]$ $A$ માંથી દાખલ થતો વિદ્યુત પ્રવાહ $I$ લો અને ચોસલામાં તે એક અર્ધ ગોળાકાર સપાટી ઉપર પ્રસરે છે. તેમ માનવામાં આવે.
$[B]$ઓહમને નિયમ $E = \rho j $ ને ઉપયાગ કરીને $A$ થી $r$ અંતરે વિદ્યુત ક્ષેત્ર $E (r)$ ગણવામાં આવે જ્યાં $j,r$ આગળ દર એકમ ક્ષેત્રફળે વિદ્યુત પ્રવાહ છે.
$[C]$ $E (r)$ નાં $r$ પરનાં આધારપણા પરથી $r$ આગળ સ્થિતિમાન $V (r)$ મેળવવામાં આવે.
$[D]$$D$ માંથી મહાર નીકળતા ($D$ ને છોડતા) વિદ્યુત પ્રવાહ $ I$ માટે $(i)$ અથવા
$B$ અને $C$ વચ્ચે માપવામાં આવતો $\Delta V$ ............ થાય.
- 6બે એકસમાન કોષોને જ્યારે સમાંતરમાં કે શ્રેણીમાં જોડવામાં આવે છે ત્યારે બાહ્ય $5\,\Omega$ ના અવરોધમાંથી સમાન પ્રવાહ આપે છે. દરેક કોષનો આંતરિક અવરોધ $...........\Omega$ હશે.View Solution
- 7એક મીટર લાંબા તારને બે અસમાન ભાગ $X$ અને $Y$માં તોડવામાં આવે છે. $X$ ભાગને લંબાવીને બીજો તાર $W$ બનાવવામાં આવે છે. $W$ તારની લંબાઈ $X$ની લંબાઈ કરતાં બમણી છે અને $W$ નો અવરોધ $Y$ના કરતાં બમણો છે. $X$ અને $Y$ની લંબાઈઓનો ગુણોત્તર શોધો.View Solution
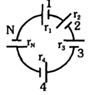
- 8આકૃતિમાં બતાવ્યા પ્રમાણે $N$ કોષોનો સમૂહ કે જેમનું $emf\ E_N = 1.5\ r_N$ સૂત્ર પ્રમાણે આંતરિક અવરોધ સાથે બદલાય છે. પરિપથમાં પ્રવાહ $I$ ................ $A$ છે.View Solution
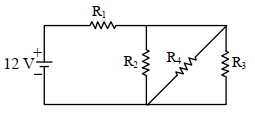
- 9આપેલ આકૃતિમાં, $\mathrm{R}_1=10 \Omega, \mathrm{R}_2=8 \Omega, \mathrm{R}_3=4 \Omega$ અને $\mathrm{R}_4=8 \Omega$ છે. બેટરી આદર્શ અને તેને $12 \mathrm{~V}$ emf છે. પરિપથ માટે સમતુલ્ય અવરોધ અને બેટરી દ્વારા પૂરો પડાતો પ્રવાહ અનુક્મે. . . . . . . . હશે.View Solution
- 10ઇલેક્ટ્રીક કીટલી દ્વારા $1$ લિટર પાણીને ગરમ કરતા $12$ મિનિટ લાગે છે, જો $20 \%$ આંટા કોઇલમાંથી દૂર કરતા $1$ લિટર પાણીને ગરમ કરતા લાગતો સમય શોધો.View Solution
