Electric field at \(\mathrm{p}=2 \mathrm{E}_{1} \cos \theta_{1}-2 \mathrm{E}_{2} \cos \theta_{2}\)
\(=\frac{2 \mathrm{Kq}}{\left(\mathrm{d}^{2}+\mathrm{D}^{2}\right)} \times \frac{\mathrm{D}}{\left(\mathrm{d}^{2}+\mathrm{D}^{2}\right)^{1 / 2}}-\frac{2 \mathrm{Kq}}{\left[(2 \mathrm{d})^{2}+\mathrm{D}^{2}\right]} \times \frac{\mathrm{D}}{\left[(2 \mathrm{d})^{2}+\mathrm{D}^{2}\right]^{1 / 2}}\)
\(=2 \mathrm{KqD}\left[\left(\mathrm{d}^{2}+\mathrm{D}^{2}\right)^{-3 / 2}-\left(4 \mathrm{d}^{2}+\mathrm{D}^{2}\right)^{-3 / 2}\right]\)
\(=\frac{2 \mathrm{KqD}}{\mathrm{D}^{3}}\left[\left(1+\frac{\mathrm{d}^{2}}{\mathrm{D}^{2}}\right)^{-3 / 2}-\left(1+\frac{4 \mathrm{d}^{2}}{\mathrm{D}^{2}}\right)^{-3 / 2}\right]\)
Applying binomial approximation \(\because \mathrm{d}<<\mathrm{D}\)
\(=\frac{2 \mathrm{KqD}}{\mathrm{D}^{3}}\left[1-\frac{3}{2} \frac{\mathrm{d}^{2}}{\mathrm{D}^{2}}-\left(1-\frac{3 \times 4 \mathrm{d}^{2}}{2 \mathrm{D}^{2}}\right)\right]\)
\(=\frac{2 \mathrm{KqD}}{\mathrm{D}^{3}}\left[\frac{12}{2} \frac{\mathrm{d}^{2}}{\mathrm{D}^{2}}-\frac{3}{2} \frac{\mathrm{d}^{2}}{\mathrm{D}^{2}}\right]\)
\(=\frac{9 \mathrm{kqd}^{2}}{\mathrm{D}^{4}}\)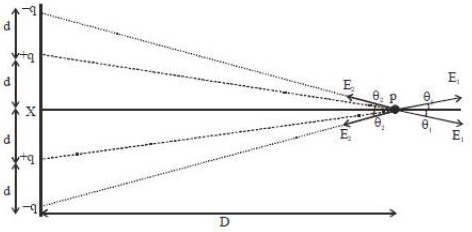
Download our appand get started for free
Similar Questions
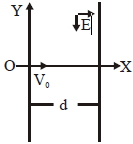
- 1એક વિજભારિત કણ ($m$ દળ અને $q$ વિજભાર) $X$ અક્ષ દિશામાં $V _{0}$ વેગથી ગતિ કરે છે.જ્યારે તે ઉગમબિંદુ પાસેથી પસાર થાય ત્યારે તે $\overrightarrow{ E }=- E \hat{ j }$ જેટલા એકસમાન વિદ્યુતક્ષેત્રમાં (જે $x = d$ સુધી પ્રવર્તે છે) દાખલ થાય છે. $x > d$ ક્ષેત્રમાં ઇલેક્ટ્રોનના ગતિપથનું સમીકરણ શું હશે?View Solution
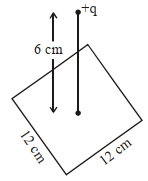
- 2આકૃત્તિમાં દર્શાવ્યા પ્રમાણે $12\, cm$ ની બાજુ ધરાવતાં એક ચોરસની શિરોલંબ ઉપર $6\, cm$ અંતરે $+\,12 \,\mu C$ નાં એક બિંદુવર વીજભાર રહેલ છે. ચોરસમાંથી પસાર થતાં વિદ્યુતફ્લકસનું મૂલ્ય ....... $\times 10^{3} \,Nm ^{2} / C$ થશે.View Solution
- 3$R$ ત્રિજ્યાનો એક ગોળો છે અને $2R$ ત્રિજ્યાનો બીજો કાલ્પનિક ગોળો કે જેનું કેન્દ્ર આપેલ ગોળાના કેન્દ્રને સુસંગત છે. જેના પરનો વિદ્યુતભાર $q$ છે. કાલ્પનિક ગોળા સાથે સંકળાયેલ ફલક્સ ........ છે.View Solution
- 4જો એક બીજાથી $d$ અંતરે રહેલા બે વીજભારો $q_1$ અને $q_2$ ડાઈલેક્ટ્રીક અચળાંક $K$ ધરાવતા માધ્યમમાં રાખેલ છે. તો તેટલા સ્થિરવિદ્યુત બળ માટે હવાના માધ્યમમાં બે વીજભારો વચ્ચેનું સમતુલ્ય અંતર કેટલું હોય ?View Solution
- 5$+\sigma_{\mathrm{s}} \mathrm{C} / \mathrm{m}^2$ જેટલી નિયમિત પૃષ્ઠ વિદ્યુતભાર ધનતા ધરાવતી એક અનંત સમતલ તક્તિને $x-y$ સમતલમાં મૂકવામાં આવે છે. બીજા એક $+\lambda_{\mathrm{e}} \mathrm{C} / \mathrm{m}$ જેટલી નિયમિત રેખીય વિધુતભાર ધનતા ધરાવતા અનંત લંબાઈના લાંબા તાર ને $z=4 \mathrm{~m}$ સમતલ અને $y$-અક્ષને સમાંતર રાખવામાં આવે છે. જો મૂલ્યોમાં $\left|\sigma_s\right|=2\left|\lambda_{\mathrm{e}}\right|$ હોય તો $(0,0,2)$ સ્થાન આગળ તક્તિ ( પૃષ્ઠ) વિદ્યુતભાર અને રેખીય વિધુત ભાર ને કારણે મળતા વિધુતક્ષેત્રનાં મૂલ્યોનો ગુણોતર. . . . . છે.View Solution
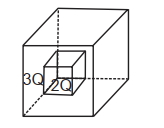
- 6આકૃતિતિાં દર્શાવ્યા અનુસાર $2 Q$ અને $3 Q$ જેટલો વિદ્યુતભાર ઘેરતા બે પોલા સમકેન્દ્રીય સમઘનો $C_1$ અને $C_2$ છે. $C_1$ અને $\mathrm{C}_2$ માંથી પસાર થતા વિદ્યુત ફ્લક્સનો ગુણોત્તર_____________છે.View Solution
- 7$1\, \mu C$ વિદ્યુતભારોને $x-$ અક્ષ પર $x = 1, 2,4, 8, .... \infty$ મૂકવામાં આવે છે. તો ઉગમ બિંદુ પર રહેલ $1\, C$ વિદ્યુતભાર પર કેટલા .....$N$ બળ લાગે?View Solution
- 8ધાતુના બે સમાન ગોળાઓ $B$ અને $C$ પર સમાન વિદ્યુતભાર છે.જયારે આ બે ગોળાઓને એકબીજાથી અમુક અંતરે રાખવામાં આવે છે,ત્યારે તેમની વચ્ચે અપાકર્ષી બળ $F$ લાગે છે.હવે,આ ગોળાઓ જેવા જ એક ત્રીજા વિદ્યુતભાર રહિત ગોળાનો $B$ સાથે સ્પર્શ કરાવી છૂટો પાડવામાં આવે છે.ત્યારબાદ તેનો $C$ સાથે સ્પર્શ કરાવી છૂટો પાડવામાં આવે છે.ગોળા $B$ અને $C$ વચ્ચે લાગતું નવું અપાકર્ષણ બળ કેટલું હશે? (બંને ગોળા વચ્ચેનું અંતર બદલાતું નથી.)View Solution
- 9$5\,\mu C$ બિંદુવત વિજભારથી $80\, cm$ અંતરે વિદ્યુતક્ષેત્રની પ્રબળતા કેટલી હશે?View Solution
- 10બે વિદ્યુતભારો $9e$ અને $3e$ એકબીજાથી $r$ અંતરે મૂકેલા છે. જ્યાં વિદ્યુતક્ષેત્રની તીવ્રતા શૂન્ય હોય તે બિંદુ ....... અંતરે આવેલા છે.View Solution
