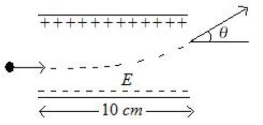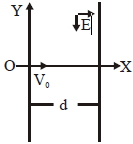
Let particle have charge \(q\) and mass \({ }^{\prime} m ^{\prime}\)
Solve for \((q,m)\) mathematically
\(F _{ x }=0, a _{ x }=0,( v )_{ x }=\) constant
time taken to reach at \(P ^{\prime}=\frac{ d }{ V _{0}}= t _{0}( let )\)\(\ldots(1)\)
(Along \(-y), y_{0}=0+\frac{1}{2} \cdot \frac{q E}{m} \cdot t_{0}^{2}....(2)\)
\(v_{x}=v_{0}\)
\(v=u+a t\) (along -ve \('y'\))
speed \(v _{ y 0}=\frac{ q E }{ m } \cdot t _{0}\)
\(\tan \theta=\frac{ v _{ y }}{ v _{ x }}=\frac{ qEt _{0}}{ m \cdot v _{ o }},\left( t _{ o }=\frac{ d }{ v _{ o }}\right)\)
\(\tan \theta=\frac{q Ed }{ m \cdot v _{0}^{2}}\)
\(\operatorname{slope}=\frac{-q \operatorname{Ed}}{m v_{0}^{2}}\)
Now we have to find eq \(^{n}\) of straight line whose slope is \(\frac{-q Ed }{ mv _{0}^{2}}\) and it pass through
point \(\rightarrow\left( d ,- y _{0}\right)\)
Because after \(x > d\)
No electric field \(\Rightarrow F _{\text {net }}=0, \overrightarrow{ v }=\) const.
\(y=m x+c,\left\{\begin{array}{l}m=\frac{q E d}{m v_{0}^{2}} \\ \left(d,-y_{0}\right)\end{array}\right\}\)
\(-y_{0}=\frac{-q E d}{m v_{0}^{2}} \cdot d+c \Rightarrow c=-y_{0}+\frac{q E d^{2}}{m v_{0}^{2}}\)
Put the value
\(y=\frac{-q E d}{m v_{0}^{2}} x-y_{0}+\frac{q E d^{2}}{m v_{0}^{2}}\)
\(y _{0}=\frac{1}{2} \cdot \frac{ qE }{ m }\left(\frac{ d }{ v _{0}}\right)^{2}=\frac{1}{2} \frac{ q Ed ^{2}}{ mv _{0}^{2}}\)
\(y =\frac{- qEdx }{ mv _{0}^{2}}-\frac{1}{2} \frac{ qEd ^{2}}{ mv _{0}^{2}}+\frac{ qEd ^{2}}{ mv _{0}^{2}}\)
\(y=\frac{-q E d}{m v_{0}^{2}} x+\frac{1}{2} \frac{q E d^{2}}{m v_{0}^{2}}\)
\(y=\frac{q E d}{m v_{0}^{2}}\left(\frac{d}{2}-x\right)\)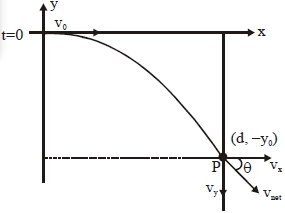
Download our appand get started for free
Similar Questions
- 1એક વિદ્યુત ડાયપોલ, $2 \,cm$ અંતરે દૂર $1 \,\mu C$ માત્રાના બે વિરૂધ્ધ વિદ્યુતભારોની બનેલી છે. આ ડાયપોલને $10^5\,N/C$ ના બાહ્ય ક્ષેત્રમાં મૂકવામાં આવી છે. ડાયપોલ પર લાગતું મહત્તમ ટોર્ક .......... $Nm$View Solution
- 2સમકેન્દ્રિય ગોળીય કવચ $A$ અને $B $ ની ત્રિજયાઓ $r_A$ અને $r_B(r_B>r_A)$ છે.તેના પર વિદ્યુતભાર $Q_A$ અને $-Q_B(|Q_B|>|Q_A|)$ છે.તો વિદ્યુતક્ષેત્ર વિરુધ્ધ અંતરનો નો આલેખ કેવો થાય?View Solution
- 3એક ચોરસનાં ચાર શિરોબિંદુઓ પર $-Q$ વિદ્યુતભાર મૂકેલો છે.અને તેના કેન્દ્ર પર $q$ વિદ્યુતભાર મૂકેલો છે. જો તંત્ર સંતુલિત અવસ્થામાં હોય, તો $q$ નું મૂલ્ય કેટલું થાય?View Solution
- 4View Solutionહાઇડ્રોજન જેવા તંત્રમાં, ઇલેક્ટ્રોન અને પ્રોટોન વચ્ચેનાં કુલ્મબિય બળ અને ગુરુત્વકર્ષણ બળનો ગુણોત્તર . . . . .ના ક્રમનો હોય છે.
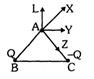
- 5આપેલ આકૃતિ માટે $A$ બિંદુ આગળ વિદ્યુતક્ષેત્રની દિશા ......... હશે.View Solution
- 6ગાઉસનો નિયમ ${ \in _0}\,\oint\limits_{} {\vec E,\,d\vec s\,\, = \,\,q} $ દ્વારા આપવામાં આવે છે જો ગાઉસિયન પૃષ્ઠ વડે ઘેરાતો ચોખ્ખો વિદ્યુતભાર શૂન્ય હોય તો .......View Solution
- 7$R$ ત્રિજ્યાનો એક ગોળો છે અને $2R$ ત્રિજ્યાનો બીજો કાલ્પનિક ગોળો કે જેનું કેન્દ્ર આપેલ ગોળાના કેન્દ્રને સુસંગત છે. જેના પરનો વિદ્યુતભાર $q$ છે. કાલ્પનિક ગોળા સાથે સંકળાયેલ ફલક્સ ........ છે.View Solution
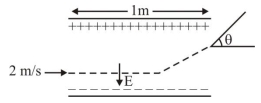
- 8આકૃતિમાં દર્શાવ્યા પ્રમાણે $1\,m$ ની પ્લેટોની લંબાઈ વાળી બે સમાંતર પ્લેટો વચ્ચે $E =(8 m / e ) V / m$ જેટલું નિયમિત વિદ્યુતક્ષેત્ર ઉત્પન્ન કરવામાં આવે છે. (જ્યાં $m =$ ઈલેકટ્રોનનું દળ, અને $e =$ ઈલેકટ્રોનનો વિદ્યુતભાર છે). એક ઈલેકટ્રોન પ્લેટોની વચ્ચે સંમિત રીતે $2\,m / s$ ની ઝડપથી દાખલ થાય છે. જ્યારે તે ક્ષેત્રની બહાર નીકળે ત્યારે ઈલેકટ્રોનના પથનું વિચલન $..............$ હશે.View Solution
- 9જો $g _{ E }$ અને $g _{ M }$ એ અનુક્રમે પૃથ્વી અને ચંદ્રની સપાટી પર ગુરુત્વપ્રવેગનાં મૂલ્યો હોય અને બંને સપાટ્ટી પર મિલિકાનનો પ્રયોગ કરવામાં આવે તો નીચેના ગુણોત્તરનું મૂલ્ય કેટલું થાય? ચંદ્ર પર વિદ્યુતભાર/પૃથ્વી પર વિદ્યુતભારView Solution
- 10બે સમાંતર પ્વેટ (તક્તિ)ની વચ્યે $10\,N/C$ નું નિયમિત વિદ્યુતક્ષેત્ર ઉત્પન્ન થાય છે. એક ઇલેક્ટોન $0.5\,eV$ ગતિઊર્જા સાથે તક્તિઓની વચ્યેના વિસ્તારમાં સંમિતિ પૂર્વક દાખલ થાય છે. દરેક તક્તિઓની લંબાઈ $10\,cm$ છે. જ્યારે ઈલેકટ્રોન આ ક્ષેત્રના વિસ્તારમાંથી બહાર નીકળે ત્યારે તેના ગતિપથના વિચલન કોણ $(\theta)$ $...........^{\circ}$ (ડિગ્રી) થશે.View Solution