$+\sigma_{\mathrm{s}} \mathrm{C} / \mathrm{m}^2$ જેટલી નિયમિત પૃષ્ઠ વિદ્યુતભાર ધનતા ધરાવતી એક અનંત સમતલ તક્તિને $x-y$ સમતલમાં મૂકવામાં આવે છે. બીજા એક $+\lambda_{\mathrm{e}} \mathrm{C} / \mathrm{m}$ જેટલી નિયમિત રેખીય વિધુતભાર ધનતા ધરાવતા અનંત લંબાઈના લાંબા તાર ને $z=4 \mathrm{~m}$ સમતલ અને $y$-અક્ષને સમાંતર રાખવામાં આવે છે. જો મૂલ્યોમાં $\left|\sigma_s\right|=2\left|\lambda_{\mathrm{e}}\right|$ હોય તો $(0,0,2)$ સ્થાન આગળ તક્તિ ( પૃષ્ઠ) વિદ્યુતભાર અને રેખીય વિધુત ભાર ને કારણે મળતા વિધુતક્ષેત્રનાં મૂલ્યોનો ગુણોતર. . . . . છે.
JEE MAIN 2024, Diffcult
a
\(\frac{\mathrm{E}_S}{\mathrm{E}_{\ell}}=\frac{\sigma}{2 \epsilon_0} \times \frac{2 \pi \epsilon_0 \mathrm{r}}{\lambda}\)
\(\frac{\mathrm{E}_S}{\mathrm{E}_{\ell}}=\frac{\sigma}{2 \epsilon_0} \times \frac{2 \pi \epsilon_0 \mathrm{r}}{\lambda}\)
\(=\frac{\pi \times \sigma \mathrm{r}}{\lambda}\)
\(=\frac{\pi \times 2 \lambda \times 2}{\lambda}=\frac{4 \pi}{1}\)
\(\therefore \mathrm{n}=16\)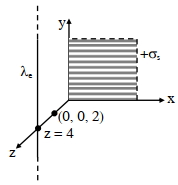
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$25.5\, k\,Vm^{-1}$ જેટલા વિદ્યુતક્ષેત્રમાં $6$ વધારાના ઇલેક્ટ્રોન ધરાવતા પ્રવાહીના ટીપાને સ્થિર રાખવામા આવે છે.પ્રવાહીની ઘનતા $1.26\times10^3\, kg\, m^{-3}$ હોય તો ટીપાની ત્રિજ્યા કેટલી હશે?View Solution
- 2સામાન્ય બિંદુએ, $l$ લંબાઇની દળરહિત દોરીઓ સાથે બે આદર્શ વિદ્યુતભારિત ગોળાઓ લટકાવ્યા છે.તેમની વચ્ચે લાગતા અપાકર્ષણનાં કારણે શરૂઆતમાં તેમની વચ્ચેનું અંતર $d \,(d << l)$ છે.બંને ગોળામાંથી વિદ્યુતભાર સમાન દરથી લીક થવાનું શરૂ થાય છે અને તેના લીધે ગોળાઓ એકબીજા તરફ $v$ વેગથી નજીક આવે છે ત્યારે ગોળા વચ્ચેનું અંતર $x$ ને વેગ $v$ ના વિધેયને કયા સ્વરૂપે મળશે?View Solution
- 3બે બિંદુવત વિદ્યુતભારો $+ 8q$ અને $-2q $ $x = 0$ અને $x = L$ આગળ મૂકેલા છે. આ બે બિંદુવત વિદ્યુતભારોને લીધે $x -$ અક્ષ પરના બિંદુ આગળ ચોખ્ખું વિદ્યુત શૂન્ય ..... હશે.View Solution
- 4દરેક ઉપર $\mathrm{Q}$ વીજભાર ધરાવતા બે એકસમાન સુવાહક ગોળા $P$ અને $\mathrm{S}$ એકબીજાને $16 \mathrm{~N}$ ના બળથી આપાકર્ષં છે. એક ત્રીજા સમાન વિદ્યુતભાર રહીત સુવાહક ગોળાને વારા ફરતી બે ગોળાઓનાં સંપર્કમાં લાવવામાં આવે છે. $P$ અને $S$ વચ્ચે નવું અપાકર્ષણ બળ. . . . . થશે.View Solution
- 5અનુક્રમે, $+ \sigma$ અને $+ \lambda$ વિદ્યુતભાર ધનતા ધરાવતા એક અનંત પૃષ્ઠ વિદ્યુતભાર અને અનંત રેખીય વિદ્યુતભારને, એકબીજાને સમાંતર $5\,m$ અંતરે રાખવામાં આવે છે. બિંદુ $P$ અને $Q$ એ રેખીય વિદ્યુતભારથી લંબઅંતરે પૃષ્ઠ તરફ અનુક્રમે $\frac{3}{\pi}\, m$ અને $\frac{4}{\pi}\,m$ અંતરે રહેલા બિંદુ છે. બિંદ્દુ $P$ અને $Q$ આગળ પરિણામી વિદ્યુતક્ષેત્ર ના મૂલ્યો અનુક્રમે $E_P$ અને $E _Q$ છે. જો $2|\sigma|=|\lambda|$ હોય, તો $\frac{E_P}{E_Q}=\frac{4}{a}$ મળે છે. $a$ નું મૂલ્ય ....... થશે.View Solution
- 6મિલિકનના ઑઇલ ડ્રોપ પ્રયોગમાં $12$ વધારાના ઇલેક્ટ્રૉન ધરાવતું એક ઑઇલ ડ્રોપ $2.55 \times 10^{4}\; N\,C ^{-1}$ ના સમાન વિદ્યુતક્ષેત્રની અસર હેઠળ સ્થિર રાખવામાં આવ્યું છે. જો ઑઇલની ઘનતા $1.26 \;g \,cm ^{-3}$ હોય તો તે ડ્રોપની ત્રિજ્યા શોધો. $\left(g=9.81\; m s ^{-2} ; e=1.60 \times 10^{-19}\; \,C \right)$View Solution
- 7આકૃતિમાં બતાવ્યા પ્રમાણે $L$ લંબાઈના અને $Q$ વિદ્યુતભાર વાળા પાતળા અવાહક સળિયા (તેની લંબાઈ પર સમાન વિતરણ થયેલ છે.) ના એક છેડાથી અંતરે એક બિંદુવત વિદ્યુતભાર મૂકેલો છે. તે બંને વચ્ચેના વિદ્યુતબળનું મૂલ્ય શોધો.View Solution
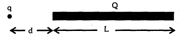
- 8View Solutionઘાતુના ગોળાને સમાન વિધુતક્ષેત્રમાં મૂકતા તેમાં વિધુતક્ષેત્ર રેખાનો સાચો માર્ગ કયો થાય?
- 9View Solutionવિદ્યુત ડાઈપોલની વિષુવ રેખા પરના એક બિંદુ માટે વિદ્યુતક્ષેત્રની તીવ્રતાની દિશા ....... છે.
- 10સમબાજુ ત્રિકોણ $ABC$ ના દરેક શિરોબિંદુ પર $ + \,q$ વિજભાર મૂકેલા છે તો $O$ બિંદુ પાસે વિદ્યુતક્ષેત્રની તીવ્રતા કેટલી થાય?View Solution