ચાર કેપેસીટર $C_1=C , C_2=2C , C_3=3 C$ અને $C_4=4C$ ને આકૃતિ દર્શાવ્યા મુજબ બેટરી સાથે જોડેલાં છે. $C_2$ અને $C_4$ ના વિદ્યુતભારનો ગુણોત્તર કેટલો થાય?
AIPMT 2005,AIIMS 2012, Medium
Download our app for free and get started
b
Equivalent capacitance for three capacitors \(\left(\mathrm{C}_{1}, \mathrm{C}_{2} \& \mathrm{C}_{3}\right)\) in series is given by
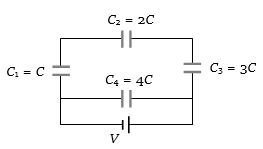
Equivalent capacitance for three capacitors \(\left(\mathrm{C}_{1}, \mathrm{C}_{2} \& \mathrm{C}_{3}\right)\) in series is given by
\(\frac{1}{\mathrm{C}_{\mathrm{eq}}}=\frac{1}{\mathrm{C}_{1}}+\frac{1}{\mathrm{C}_{2}}+\frac{1}{\mathrm{C}_{3}}=\frac{\mathrm{C}_{2} \mathrm{C}_{3}+\mathrm{C}_{3} \mathrm{C}_{1}+\mathrm{C}_{1} \mathrm{C}_{2}}{\mathrm{C}_{1} \mathrm{C}_{2} \mathrm{C}_{3}}\)
\(\Rightarrow\) \(C_{\mathrm{eq}}=\frac{\mathrm{C}_{1} \mathrm{C}_{2} \mathrm{C}_{3}}{\mathrm{C}_{1} \mathrm{C}_{2}+\mathrm{C}_{2} \mathrm{C}_{3}+\mathrm{C}_{3} \mathrm{C}_{1}}\)
\(C_{\mathrm{eq}}=\frac{C(2 C)(3 \mathrm{C})}{C(2 \mathrm{C})+(2 \mathrm{C})(3 \mathrm{C})+(3 \mathrm{C}) \mathrm{C}}=\frac{6}{11}\, \mathrm{C}\)
Charge on capacitors \(({C_1},{C_2}\& {C_3})\)
in series \(=\mathrm{C}_{\mathrm{eq}} \mathrm{V}=\frac{6 \mathrm{C}}{11} \mathrm{V}\)
Charge on capacitor \(C_{4}=C_{4} V=4 C V\)
\(\frac{\text { Charge on } \mathrm{C}_{2}}{\text { Charge on } \mathrm{C}_{4}}=\frac{\frac{6 \mathrm{C}}{11} \mathrm{V}}{4 \mathrm{CV}}=\frac{6}{11} \times \frac{1}{4}=\frac{3}{22}\)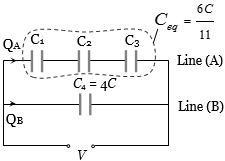
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$+q$ અને $-q$ વિદ્યુતભારો બિંદુ $A$ અને $ B$ આગળ $2L$ અંતરે મૂકેલા છે. $C$ એ $A$ અને $B$ ની વચ્ચેનું મધ્યબિંદુ છે. $+Q$ વિદ્યુતભારને અર્ધ વર્તૂળ $CRD$ માર્ગ ગતિ કરવા માટે થતું કાર્ય ....... છે.View Solution
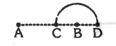
- 2View Solutionકેપેસિટરને બેટરી વડે ચાર્જ કરેલ છે.હવે બેટરી દૂર કરીને બીજા સમાન વિદ્યુતભારરહિત કેપેસિટર સાથે સમાંતરમાં જોડવામાં આવે છે. તંત્રની કુલ સ્થિતવિદ્યુતઊર્જા .....
- 3સમાંતરમાં જોડેલા સંઘારકો $C _1=1\,\mu F , C _2=2\,\mu F , C _3=4\,\mu F$ અને $C _4=3\,\mu F$ નાં તંત્રમાં કુલ વિદ્યુતભાર $....... \mu C$ હશે.(આ સંયોજનને $20\,V$ ની બેટરી જોડેલ છે તેમ ધારો)View Solution
- 4View Solutionઊગમબિંદુ આગળ આપેલ વિદ્યુતભારના વિતરણ માટે સ્થિતિમાન શોધો.
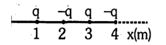
- 5$\mathrm{C}_{1}$ અને $\mathrm{C}_{2}$ કેપેસીટરને સમાંતરમાં જોડતા સમતુલ્ય કેપેસીટન્સ $10\; \mu \mathrm{F}$ મળે છે.જ્યારે તેને અલગ અલગ $1\; \mathrm{V}$ ની બેટરી સાથે જોડવામાં આવે ત્યારે $\mathrm{C}_{2}$ માં સંગ્રહાતી ઉર્જા $\mathrm{C}_{1}$ માં સંગ્રહાતી ઉર્જા કરતાં $4$ ગણી હોય છે જો આ બંને કેપેસીટરને શ્રેણીમાં જોડવામાં આવે તો સમતુલ્ય કેપેસીટન્સ કેટલો થાય?View Solution
- 6$10^{-6} \mu \mathrm{C}$ નો એક વીજભાર $X-Y$ યામ પધ્ધતિના ઉગમબિંદુ $(0,0) \mathrm{m}$ પર મૂકેલો છે. બિંદુઓ $\mathrm{P}$ અને $\mathrm{Q}$ અનુક્રમે $(\sqrt{3}, \sqrt{3}) \mathrm{m}$ અને $(\sqrt{6}, 0) \mathrm{m}$ પર રહેલા છે. બિંદુઓ$\mathrm{P}$ અને $\mathrm{Q}$ વચચેનો સ્થિતિમાન તફાવત_____થશે.View Solution
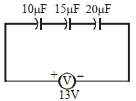
- 7આકૃતિમાં દર્શાવ્યા અનુસાર $15 \,\mu F$ ના સંધારક પરનો વિદ્યુતભાર ............ $\mu c$ હશે.View Solution
- 8$4\;V$ વિદ્યુતસ્થિતિમાનથી ચાર્જ કરેલા $C_1$ કેપેસીટરની ક્ષમતા ધરાવતા $n_1$ કેપેસીટરને શ્રેણીમાં જોડેલા છે. જ્યારે બીજા $V$ વિદ્યુતસ્થિતિમાનથી ચાર્જ કરેલા $C_2$ કેપેસીટરની ક્ષમતા ધરાવતા $n_2$ કેપેસીટરને સમાંતરમાં જોડવામાં આવે ત્યારે તેમાં સંગ્રહ થતી કુલ ઉર્જા પહેલા જોડાણમા સંગ્રહ થતી ઉર્જા જેટલી છે. તો $C_2$ નું મૂલ્ય $C_1$ ના પદમાં કેટલું થાય?View Solution
- 9$Millikan's$ ના તેલના ટીપાના પ્રયોગમાં $Q$ વિદ્યુતભારને બે પ્લેટો વચ્ચે $2400\, V$ ના વિદ્યુતસ્થીતીમાનના તફાવત હેઠળ સ્થીર રાખેલ છે બીજા અડધી ત્રિજ્યા ધરાવતા ટીપાંને સ્થીર રાખવા માટે $600\,V$ નો વિદ્યુત સ્થીતીમાનનો જરૂરી છે તો બીજા ટીપા પરનો વિદ્યુતભાર....View Solution
- 10આપેલ આકૃતિમાં વિદ્યુતભાર ધનતા $+\sigma$ અને $-\sigma$ ધરાવતી બે પ્લેટો અનુક્રમે $A$ અને $B$ દર્શાવેલ છે ક્યાં વિસ્તારમાં વિદ્યુત તીવ્રતા શૂન્ય હશે?View Solution
