ક્રમ પ્રક્મ માટે $\Delta G^o$ શોધો
.... .............$\mathrm{kJ} \mathrm{mol}^{-1}$
$2H^+ + 2e^- + \frac{1}{2}O_2\longrightarrow H_2O_{(l)} ; $
$E^o = +1.23\, V$
$Fe^{2+} + 2e^- \longrightarrow Fe_{(s)} ;\ E^o = -0.44\,V$
(a) \(Fe(s) \longrightarrow Fe^{2+}+ 2e^-\;\; ; \;\; \Delta G_1^o\)
\( {2{H^ + } + 2{e^ - } + \frac{1}{2}{O_2}\, \longrightarrow \,\,{H_2}O(l)\,\,;\,\,\Delta G_2^o} \)
____________________________________________
\( Fe(s) + 2H^+ + \frac{1}{2} O_2 \longrightarrow Fe^{2+}+ H_2O \;\;; \;\; \Delta G_3^o\)
Applying, \(\Delta G_1^o + \Delta G_2^o = \Delta G_3^o\)
\(\Delta G_3^o = (-2F \times 0.44) + (-2F \times 1.23)\)
\(\Delta G_3^o = -(2 \times 96500 \times 0.44+ 2 \times 96500 \times 1.23)\)
\(\Delta G_3^o = -322310\, J\)
\(\Delta G_3^o= -322 \,KJ\)
Download our appand get started for free
Similar Questions
- 1$4\,cm^{2}$ આડછેદના ક્ષેત્રફળવાળા ધ્રુવ સાથે વાહકતા કોષમાં શુદ્ધ પાણીની વાહકતા $2\,cm$ અંતરે મુકેલી છે. જે $8 × 10^{-7}\, S \,cm^{-1}$ છે. તો પાણીનો અવરોધ....View Solution
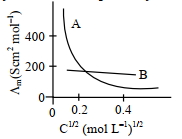
- 2વિધૂતવિભાજયો $A$ અને $B$ માટે મોલર વાહકતાઓ વિરુધ્ધ $C C1/2$ નો ગ્રાફ (આલેખ) નીચે દર્શાવેલ છે. વિધુતવિભાજ્યો $A$અને $B$ અનુક્રમે શોધો :View Solution
- 3પિગલીત $NaCl$ ના વિદ્યુત વિભાજનમાં એનોડ પર......View Solution
- 4સ્વયંભૂ પ્રક્રિયા માટે $\Delta G$ , સંતુલન અચળાંક $ (K)$ અને $E_{Cell}^o$ અનુક્રમે . . . . હશે.View Solution
- 5$1\,\,M$ બેન્ઝોઇક ઍસિડ ની તુલ્યવાહકતા $12.8$ મ્હો સેમી$^{2}$ ગ્રામ તુલ્ય$^{-1}$ છે તેમજ બેન્ઝોએટ આયન અને $H^{+}$ આયનની વાહકતા અનુક્રમે $42$ અને $288.42$ ઓહમ$^{-1}$ સેમી$^{2}$ છે, તો વિયોજન અંશ …......... $\%$View Solution
- 6${Cu}({s})\left|{Cu}^{2+}({aq})(0.1 {M}) \| {Ag}^{+}({aq})(0.01 {M})\right| {Ag}({s})$ કોષ માટે,કોષનો પોટેન્શિયલ ${E}_{1}=0.3095\, {~V}$View Solution
${Cu}({s})\left|{Cu}^{2+}({aq})(0.01 {M}) \| {Ag}^{+}({aq})(0.001 {M})\right| {Ag}({s})$ કોષ માટે ,કોષનો પોટેન્શિયલ $=.....\times 10^{-2} {~V}$
[ઉપયોગ : $\frac{2.303 {RT}}{{F}}=0.059$ ]
- 7બટન કોષ $A g-Z n$ માટે $Z n(s)+A g_{2} O(s) \operatorname{Zn} O(s)+2 A g(s)$ ચોખ્ખી પ્રક્રિયા છેView Solution
$\Delta G_{f}^{o}\left(A g_{2} O\right)=-11.21\, kJ\,mol ^{-1}$
$\Delta G_{f}^{o}(Z n O)=-318.3\, kJ \,mol ^{-1}$
ત્યારે $E^{o}$કોષ નો બટન શેલ.........$V$ શું હશે ?
- 8View Solutionએક વિદ્યૃતરાસાણિક કોષ નું વિદ્યૃતવિભાજનીય કોષ માં કેવી રીતે પરિવર્તન કરી શકાય છે ?
- 9$AgNO_3, AgCl$ અને $NaCl$ અનંત મંદને મોલર વાહકતા $116.5, 121.6$ અને $110.3$ છે. તો $NaNO_3$ ની મોલર વાહકતા એ...View Solution
- 10$Na,\,\,Hg,\,\,S,\,\,Pt$ અને ગ્રેફાઇટમાંથી કયા પદાર્થો જલીય દ્રાવણ ધરાવતા વિદ્યુત વિભાજય કોષોમાં વિદ્યુતધ્રુવ તરીકે વાપરી શકાય છે?View Solution
