Given that,
\(\ln k\left(s^{-1}\right)=14.34-\frac{1.25 \times 10^{4}}{T} K \ldots(i)\)
We know that,
\(\ln k\left(s^{-1}\right)=\ln A-\frac{E_{a}}{R T} \ldots( ii )\)
On comparing equation \((i)\) and \((ii)\), we get
\(\frac{E_{a}}{R}=1.25 \times 10^{4} \,K\)
\(\therefore E_{a}=1.25 \times 10^{4} K \times R\) \(cal\) \(K^{-1} mol ^{-1}\)
\(=1.25 \times 10^{4} K \times 2\) \(cal\) \(K^{-1} mol ^{-1}\)
\(\left[\because R=2 \operatorname{cal} K^{-1} mol ^{-1}\right]\)
\(=2.50 \times 10^{4}\) \(cal\) \(mol ^{-1}\)
Download our appand get started for free
Similar Questions
- 1વાયુરૂપ ઘટકો વચ્ચેની પ્રક્રિયા : $2A + B\rightarrow C + D. $ માટે પ્રક્રિયા વેગ $= K[A][B] $ છે. તો પહેલા કરતા પાત્રનું $1/4$ કદ જેટલુ ઓછુ લેવામાં આવે તો પહેલાના પ્રક્રિયા વેગ કરતાં અંતિમ પ્રક્રિયા વેગ કેટલા ગણો મળશે ?View Solution
- 2રાસાયણિક ગતિકીમાં સમીકરણ $K = A{e^{ - {E_a}/RT}}$ ના સંદર્ભમાં નીચેનામાંથી ક્યુ વિધાન સાચું છે ?View Solution
- 3$A\rightarrow$ નિપજ ચોક્કસ પ્રક્રિયાનો અર્ધઆયુ સમય $1$ કલાક છે. જ્યારે પ્રક્રિયક $ 'A' $ ની શરૂઆતની સાંદ્રતા $2.0$ મોલ $L^{-1}$ હોય તો જો શૂન્ય ક્રમની પ્રક્રિયા હોય તો તેની સાંદ્રતા $0.50$ થી $0.25$ મોલ $L^{-1}$ સુધી આવતાં ......... $h$ લેશે.View Solution
- 4એક પ્રક્રિયા $2$ કલાકમાં $50 \%$ પૂર્ણ થાય છે. તથા $4$ કલાક માં $75 \%$ પૂર્ણ થાય છે. તો પ્રક્રિયાનો ક્રમ ..........View Solution
- 5એક પ્રક્રિયા નો અર્ધ આયુષ્ય સમય $1\,min.$ છે તો $99.9\, \%$ પ્રક્રિયાને પૂર્ણ થવા માટે લાગતો જરૂરી સમય ......... $min.$ છે [ઉપયોગ : $\ln\, 2=0.69, \ln \,10=2.3]$View Solution
- 6સમાન તાપમાન પર એક પ્રક્રિયા ત્રણ તબકકકાઓમાં થાય છે. સમગ્ર વેગ અચળાંક $K=\frac{K_1 K_2}{K_3}$ છે. જો $\mathrm{Ea}_1, \mathrm{Ea}_2$ અને $Еаз$ એં અનુક્મે $40,50$ અને $60 \mathrm{~kJ} / \mathrm{mol}$ હોય તો, સમગ્ર Ea $\mathrm{kJ} / \mathrm{mol}$છે.View Solution
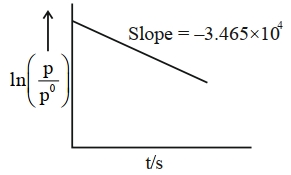
- 7એઝોમિથેનના વિધટન માટે,View Solution
$CH _3 N _2 CH _3( g ) \rightarrow CH _3 CH _3( g )+ N _2( g )$
આ એક પ્રથમક્રમ પ્રક્રિયા છે. $600\, K$ પર સમય સાથે આંશિક દબાણમાં વિવિધતા નીચે આપેલ છે. પ્રક્રિયાનો અર્ધ આયુષ્ય $\times 10^{-5}\, s$ છે. [નજીકનો પૂર્ણાંક]
- 8ચોક્કસ પ્રક્રિયા માટેનો પ્રથમ ક્રમની પ્રકિયાનો વેગ અચળાંક $1.667 \times 10^{-6}\, s^{-1}$ $727\,^oC$ તાપમાને થી $1.667 \times 10^{-4}\,s^{-1}$ તાપમાને $1571\,^oC$.આપેલ તાપમાન શ્રેણી ઉપર સક્રિયકરણ ઉર્જાની સ્થાયિતા ધારીને, કયા $1150\,^oC$, પર દર સતત છેView Solution
- 9નીચે આપેલ દર અચળાંક $(k)$ સાથે તાપમાન $(T)$ વચ્ચેનો તફાવત આલેખમાં દર્શાવ્યો છે. તો કયો આલેખ આર્હેંનિયસ સમીકરણનું પાલન કરે છે.View Solution
- 10વાતાવરણના ઉપરના સ્તરમાં ઓઝોન વિઘટન નાઇટ્રિક ઓક્સાઇડ દ્વારા ઉદ્દીપિત થાય છે. પ્રક્રિયાની ક્રિયાવિધિ નીચે મુજબ છે.View Solution
$2NO \rightleftharpoons {N_2}O + \left[ O \right]$
${O_3} + \left[ O \right] \to 2{O_2}\,(slow)$
તો પ્રકિયાનો કમ જણાવો.
