એઝોમિથેનના વિધટન માટે,
$CH _3 N _2 CH _3( g ) \rightarrow CH _3 CH _3( g )+ N _2( g )$
આ એક પ્રથમક્રમ પ્રક્રિયા છે. $600\, K$ પર સમય સાથે આંશિક દબાણમાં વિવિધતા નીચે આપેલ છે. પ્રક્રિયાનો અર્ધ આયુષ્ય $\times 10^{-5}\, s$ છે. [નજીકનો પૂર્ણાંક]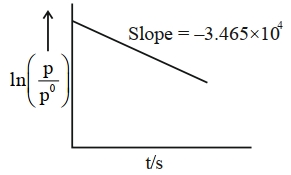
JEE MAIN 2022, Medium
Download our app for free and get started
b
For first order reaction
For first order reaction
$k =\frac{1}{ t } \ln \left(\frac{ P _{0}}{ P }\right)$
$\ln \left(\frac{ P _{0}}{ P }\right)= kt$
$t _{1 / 2}=\frac{\ln 2}{ k }=\frac{0.693}{3.465 \times 10^{4}}=2 \times 10^{-5}$
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1દૂધનો એક નમૂનો, જયારે તેમાં lactobacillus acidophilus ની સંખ્યા બમણી થાય ત્યારે, $300$ $K$ પર $60$ $min$ માં ફાટી જાય (splits) છે અને $400$ $K$ પર $40$ $min$ માં ફાટી જાય છે. આ પ્રક્રિયા માટેની સક્રિયકરણ ઊર્જા ( in $\mathrm{kJ/mole}$ ) ....... ની નજીક છે.View Solution
$\left( {{\rm{R}} = 8.3\;{\rm{Jmo}}{{\rm{l}}^{ - 1}}{{\rm{K}}^{ - 1}},\ln \left( {\frac{2}{3}} \right) = 0.4,\left. {{e^{ - 3}} = 4.0} \right)} \right.$
- 2તાપમાન સાથે પ્રક્રિયાનો વેગ અચળાંક નીચેના સમીકરણ મુજબ બદલાય છે. $\log \,K = $ constant $ - {E_a}/2.303\,RT$ જો $\log \,K \to 1/T$ નો આલેખ $- 5632$ જેટલો ઢાળ ધરાવતી સીધી રેખા મળે, તો પ્રક્યિાની સક્રિયકરણ ઊર્જા .......... $kJ\, mol^{-1}$ મળશે.View Solution
- 3પ્રક્રિયા $3A+2B \to C + D$ માટે વિકલનીય વેગ નિયમ ....તરીકે લખાશે.View Solution
- 4રાસાયણિક પ્રકિયા ની સક્રિયકરણ ર્જા $(E_a)$ અને અચળ વેગ $(k_1$ અને $ k_2)$ બે જુદા જુદા તાપમાને પ્રક્રિયા $(T_1$ અને $T_2)$ કોના દ્વારા સંબંધિત છેView Solution
- 5નીચેની પ્રક્રિયા $xA \longrightarrow yB$ માં $“A”$ અને $“B”$ અનુક્રમે શુ હોઇ શકે ?View Solution
${\log _{10}}\,\left[ { - \frac{{d\left[ A \right]}}{{dt}}} \right] = {\log _{10}}\,\left[ {\frac{{d\left[ B \right]}}{{dt}}} \right] + 0.3010$
- 6અચળ ક્દે વાયુ $A$ નાં પ્રથમ ક્રમના ઉષ્મીય વિઘટન દરમિયાન નીચે મુજબ માહિતી પ્રાપ્ત થાય છે.View Solution
$\mathrm{A}(\mathrm{g}) \rightarrow 2 \mathrm{~B}(\mathrm{~g})+\mathrm{C}(\mathrm{g})$
$S.\ No$ સમય/s કુલ દબાણ/(atm)
$1.$ $0$ $0.1$
$2.$ $115$ $0.28$
પ્રક્રિયાનો વેગ અચળાંક _______________$\times 10^{-2} \mathrm{~s}^{-1}$ (નજીકનાં પૂનાંકમાં)
- 7$A + B \rightarrow $ નિપજ, પ્રક્રિયા માટે $A$ ના સંદર્ભમાં ક્રમ $1$ છે અને $B$ ના સંદર્ભમાં ક્રમ $1/2 $ છે. જ્યારે $A$ અને $B$ બંનેની સાંદ્રતા ચાર ગણી વધે છે. તો દર એ ....... ગુણાંક વધે છે.View Solution
- 8કાલ્પનિક પ્રક્રિયા $A_2 + B_2 \rightarrow2AB$ નીચે મુજબ ક્રિયાવિધી દર્શાવે છે. તો બધી જ પ્રક્રિયાનો ક્રમ .... થાય.View Solution
$A_2 $ $\rightleftharpoons$ $ A + A$ ....... (ઝડપી) ;
$A + B_2\rightarrow AB + B$ ..... (ધીમી) ;
$ A + B \rightarrow AB$ ...... (ઝડપી)
- 9પ્ર્કિયકની શરૂઆતની સાંદ્રતા $0.02\, M$ ધરાવતા એક શૂન્ય ક્રમની પ્રક્રિયાનો અર્ધઆયુષ્ય સમય $100\, s$ છે. તો પ્રક્રિયા માટે વેગ અચળાંક ($mol\, L ^{-1} s ^{-1}$ માં$)$ જણાવો.View Solution
- 10રસાયણિક પ્રક્રિયા $A+B \rightarrow$ નીપજ માટે,$A$ અને $B$ ના સંદર્ભ સાથે ક્રમ $1$ છેView Solution
Rate $mol\,L^{-1}\,s^{-1}$ $[A]$ $mol\,L^{-1}$ $[B]$ $mol\,L^{-1}$ $0.10$ $20$ $0.5$ $0.40$ $x$ $0.5$ $0.80$ $40$ $y$ $x$ અને $y$ ના મુલ્યો શું છે ?