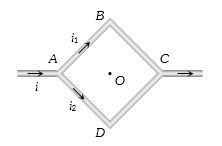
(b) According to question resistance of wire \(ADC\) is twice that of wire \(ABC\). Hence current flows through \(ADC\) is half that of \(ABC\) i.e. \(\frac{{{i_2}}}{{{i_1}}} = \frac{1}{2}\). Also \({i_1} + {i_2} = i\) \(==>\) \({i_1} = \frac{{2i}}{3}\) and \({i_2} = \frac{i}{3}\)
Magnetic field at centre \(O\) due to wire \(AB\) and \(BC\) (part \(1\) and \(2\)) \({B_1} = {B_2} = \frac{{{\mu _0}}}{{4\pi }}.\frac{{2{i_1}\sin {{45}^o}}}{{a/2}} \otimes \)\( = \frac{{{\mu _0}}}{{4\pi }}.\frac{{2\sqrt 2 \,{i_1}}}{a} \otimes \)
and magnetic field at centre \(O\) due to wires \(AD\) and \(DC\) (i.e. part \(3\) and \(4\)) \({B_3} = {B_4} = \frac{{{\mu _0}}}{{4\pi }}\frac{{2\sqrt 2 \,{i_2}}}{a}\odot\)
Also \(i_1 = 2i_2. \,So \,(B_1 = B_2) > (B_3 = B_4)\)
Hence net magnetic field at centre \(O\)
\({B_{net}} = ({B_1} + {B_2}) - ({B_3} + {B_4})\)
\( = 2 \times \frac{{{\mu _0}}}{{4\pi }}.\frac{{2\sqrt 2 \, \times \left( {\frac{2}{3}i} \right)}}{a} - \frac{{{\mu _0}}}{{4\pi }}.\frac{{2\sqrt 2 \,\left( {\frac{i}{3}} \right) \times 2}}{a}\)
\( = \frac{{{\mu _0}}}{{4\pi }}.\frac{{4\sqrt 2 \,i}}{{3a}}(2 - 1)\, \otimes = \frac{{\sqrt 2 \,{\mu _0}i}}{{3\pi \,a}} \otimes \)
Download our appand get started for free
Similar Questions
- 1એક અર્ધવત્તુળાકાર રીંગના આકારનો આડછેદ ધરાવતાં અતિ લાંબા તારમાથી પ્રવાહ $I$ પસાર થાય છે. રીંગની ત્રિજ્યા $R$ છે. તો તારની અક્ષ પર ઉત્પન્ન થતા ચુંબકીય પ્રેરણનું મૂલ્ય કેટલું હશે?View Solution
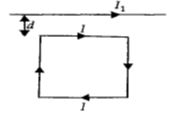
- 2આકૃતિમાં દર્શાવ્યા પ્રમાણે $I$ પ્રવાહધારીત એક ચોરસ લૂપને $I_1$ સ્થાયી પ્રવાહ પસાર કરતાં લાંબા વાહકની નજીક સમક્ષિતિજ સમતલમાં મુકેલ છે. તો લૂપ શું અનુભવે?View Solution
- 3એક $L$ મીટર લંબાઇ અને $I$ એમ્પિયર પ્રવાહધારીતા તારને વર્તુળાકાર રીતે વાળવામાં આવે તો ચુંબકીય મોમેન્ટ ........... મળેView Solution
- 4ટોરોઈડમાં એકમ લંબાઈ દીઠ આંટાઓની સંખ્યા $1000$ છે અને તેમાંથી પસાર થતો વિદ્યુતપ્રવાહ $\frac{1}{4 \pi}$ એમ્પિયર છે. અંદરની બાજુએ ઉત્પન્ન થતું ચુંબકીય ક્ષેત્ર $\left(\right.$વેબર/ $\left.m ^2\right)$ માં કેટલું હશે ?View Solution
- 5એક વિદ્યુતભાર $Q$ એ ચુંબકીય ક્ષેત્ર $\overrightarrow{ B }$ માં $\overrightarrow{d l}$ જેટલું અંતર કાપે (ગતિ કરે) છે. $\overrightarrow{ B }$ દ્વારા થતું કાર્ય શોધો :View Solution
- 6$y=0$ અને $y = d$ વચ્ચેનો વિસ્તાર ચુંબકીય ક્ષેત્ર $\vec B = B\hat z$ ધરાવે છે. $m$ દળ અને $q$ વિજભાર ધરાવતો એક કણ $\vec v = v\hat i$ વેગથી આ વિસ્તારમાં પ્રવેશે છે. જો $d = \frac{{mv}}{{2qB}}$ , હોય તો આ વિસ્તારની બીજી બાજુએ નિર્ગમન બિંદુએ વિજભારીત કણનો પ્રવેગ કેટલો હશે?View Solution
- 7એક વિદ્યુતભાર માટે $q/m$ નું મૂલ્ય $10^8\, C/kg$ અને તે $3 \times 10^5\, m/s$ ના વેગથી $0.3\, T$ તીવ્રતાવાળા ચુંબકીયક્ષેત્રમાં, ક્ષેત્ર સાથે $30^o$ ના ખૂણે દાખલ થાય છે. વક્રાકાર માર્ગની ત્રિજયા ........ $cm$ હશે.View Solution
- 8$-2\;\mu C\;$ વિદ્યુતભાર ધરાવતો કણ $2\;T$ ચુંબકીયક્ષેત્રમાં $y$ દિશામાં દાખલ થાય, જ્યારે તેનો વેગ $\left( {2\hat i + 3\hat j} \right) \times \;{10^6}\,m/s$ ત્યારે તેના પર લાગતું ચુંબકીય બળ .....View Solution
- 9View Solutionઅનંત લાંબા, સીધા પ્રવાહધારીત વાહકને કારણે બનતી ચુંબકીય ક્ષેત્ર રેખાઓનો આકાર કેવો હોય?
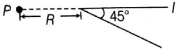
- 10$I$ પ્રવાહધારિત લાંબા તારના મધ્યબિંદુ એ $45^{\circ}$ વાળીને આકૃતિ મુજબ મુકેલ છે.મધ્યબિંદુથી $R$ અંતરે રહેલા $P$ બિંદુએ ચુંબકીય ક્ષેત્ર (ટેસ્લા માં) કેટલું થશે?View Solution