D and E are points on the sides AB and AC respectively of a $\triangle\text{ABC}.$ In the following cases, determine whether DE || BC or not. AD = 7.2cm, AE = 6.4cm, AB = 12cm and AC = 10cm.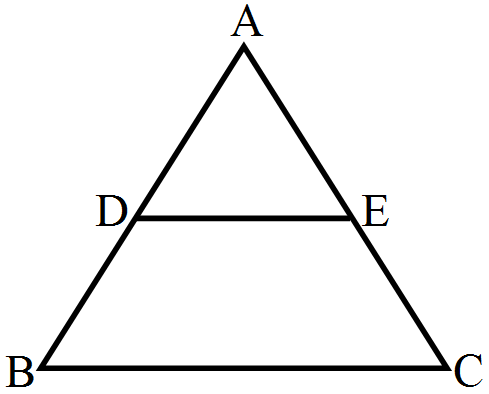

We have:
AD = 7.2cm, AB = 12cm
Therefore,
DB = 12 - 7.2 = 4.8cm
Similarly,
AE = 6.4cm, AC = 10cm
Therefore,
EC = 10 - 6.4 = 3.6cm
Now,
$\frac{\text{AD}}{\text{DB}}=\frac{7.2}{4.8}=\frac{3}{2}$
$\frac{\text{AE}}{\text{EC}}=\frac{6.4}{3.6}=\frac{16}{9}$
Thus, $\frac{\text{AD}}{\text{DB}}\not=\frac{\text{AE}}{\text{EC}}$
Applying the converse of Thalse' theorem, we conclude thet DE is not parallel to BC.
AD = 7.2cm, AB = 12cm
Therefore,
DB = 12 - 7.2 = 4.8cm
Similarly,
AE = 6.4cm, AC = 10cm
Therefore,
EC = 10 - 6.4 = 3.6cm
Now,
$\frac{\text{AD}}{\text{DB}}=\frac{7.2}{4.8}=\frac{3}{2}$
$\frac{\text{AE}}{\text{EC}}=\frac{6.4}{3.6}=\frac{16}{9}$
Thus, $\frac{\text{AD}}{\text{DB}}\not=\frac{\text{AE}}{\text{EC}}$
Applying the converse of Thalse' theorem, we conclude thet DE is not parallel to BC.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1A man goes $10\ m$ due south and then $24\ m$ due west. How far is he from the starting point?View Solution
- 2In the given figure, $\triangle\text{ODC}\sim\triangle\text{OBA},\angle\text{BOC}=115^\circ$ and $\angle\text{CDO}=70^\circ.$View Solution
Find- $\angle\text{DOC}$
- $\angle\text{DCO}$
- $\angle\text{OAB}$
- $\angle\text{OBA}$
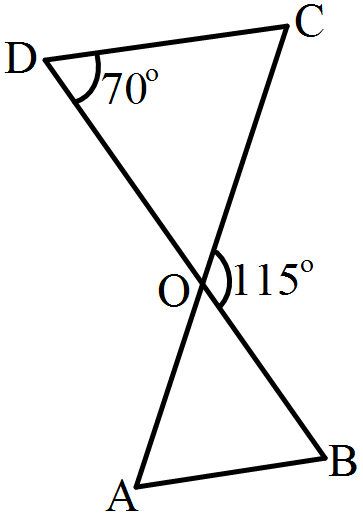
- 3View SolutionThe sides of certain triangles are given below. Determine them are right triangles:
9cm, 16cm, 18cm. - 4If the lengths of the sides BC, CA and AB of a $\triangle\text{ABC}$ are a, b and c respectively and AD is the bisectore of $\angle\text{A}$ then find the lengths of BD and DC.View Solution
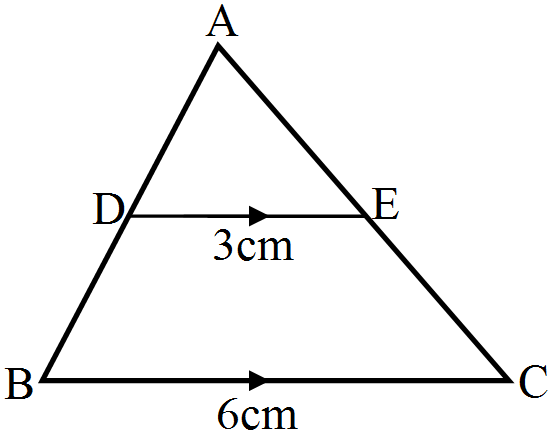
- 5In the given figure, $DE || BC$. If $DE = 3\ cm$, $BC = 6\ cm$ and $\text{ar}(\triangle\text{ADE})=15\text{cm}^2,$ find the area of $\triangle\text{ABC}.$View Solution
- 6View SolutionFor the following statments state whether true (T) or false(F):
Any two rectangles are similar. - 7$\triangle\text{ABC}\sim\triangle\text{PQR}$ and $\text{ar}(\triangle\text{ABC})=4\text{ar}(\triangle\text{PQR}).$ If BC 12cm, find QR.View Solution
- 8In a trapezium ABCD, it is given that AB || CD and AB = 2CD. Its diagonals AC and BD intersect at the point O such that $\text{ar}(\triangle\text{AOB})=84\text{cm}^2.$ Find $\text{ar}(\triangle\text{COD}).$View Solution
- 9D and E are points on the sides AB and AC respectively of a $\triangle\text{ABC}.$ In the following cases, determine whether DE || BC or not.View Solution
AB = 10.8cm, AD = 6.3cm, AC = 9.6cm and EC = 4cm.
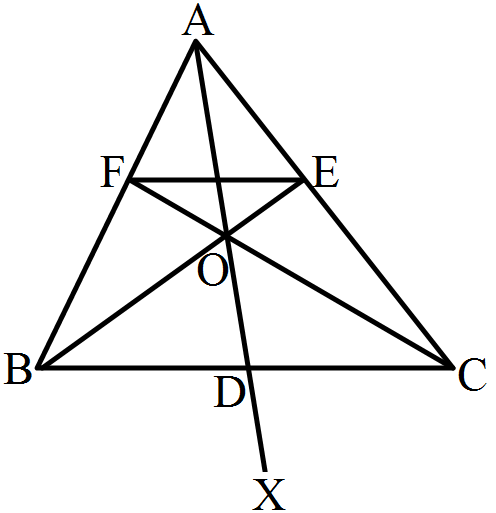
- 10In the given figure, side BC of $\triangle\text{ABC}$ is bisected at D and O is any point on AD. BO and CO produced meet AC and AB at E and F respectively, and AD is produced to X so that D is the midpoint of OX Prove that AO : AX = AF : AB and show that EF || BC.View Solution