The sides of certain triangles are given below. Determine them are right triangles:
9cm, 16cm, 18cm.
9cm, 16cm, 18cm.
For a given triangle to be a right angled, the sum of the squares of the two sides must be equal to the square of the largest side.
Let a = 9cm, b = 16cm and c= 18cm. Then
$\Big(\text{a}^2+\text{b}^2\Big)=\Big[9^2+(16)^2\Big]$
$=(81+256)\text{cm}^2$
$=337\text{cm}^2$
and $\text{c}^2=(18)^2\text{cm}^2=324\text{cm}^2$
$\therefore\big(\text{a}^2+\text{b}^2\big)\not=\text{c}^2$
Hence the given triangle is not right angled.
Let a = 9cm, b = 16cm and c= 18cm. Then
$\Big(\text{a}^2+\text{b}^2\Big)=\Big[9^2+(16)^2\Big]$
$=(81+256)\text{cm}^2$
$=337\text{cm}^2$
and $\text{c}^2=(18)^2\text{cm}^2=324\text{cm}^2$
$\therefore\big(\text{a}^2+\text{b}^2\big)\not=\text{c}^2$
Hence the given triangle is not right angled.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$\triangle\text{ABC}\sim\triangle\text{PQR}$ and $\text{ar}(\triangle\text{ABC})=4\text{ar}(\triangle\text{PQR}).$ If BC 12cm, find QR.View Solution
- 2View SolutionFind the height of an equilateral triangle of side 12cm.
- 3$\triangle\text{ABC}\sim\triangle\text{DEF}$ such that $\text{ar}(\triangle\text{ABC})=64\text{cm}^2$ and $\text{ar}(\triangle\text{DEF})=169\text{cm}^2.$ If BC = 4cm, find EF.View Solution
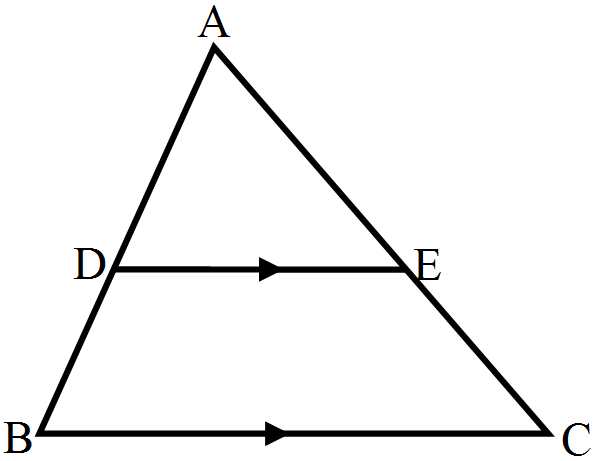
- 4D and E are points on the sides AB and AC respectively of a $\triangle\text{ABC}$ such that DE || BC:View Solution
If AD = 3.6cm, AB = 10cm and AE = 4.5cm, find EC and AC.
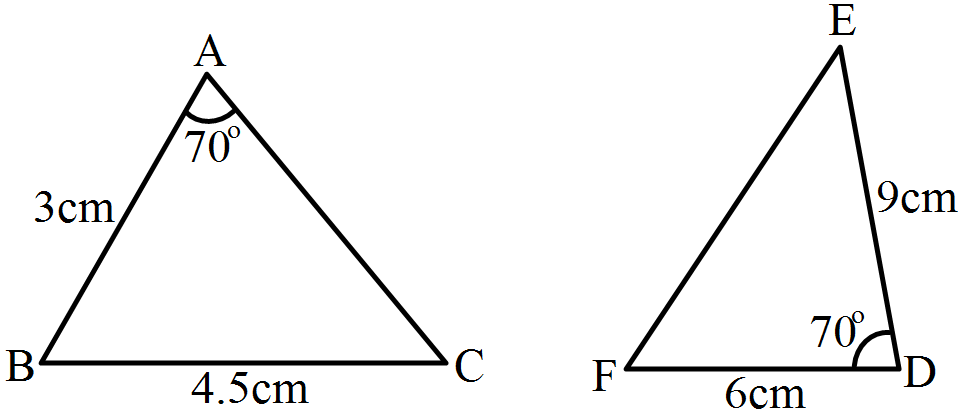
- 5View SolutionIn the given pairs of triangles, find which pair of triangles are similar. State the similarity criterior and write the similarity relation in symbolic from.
- 6View SolutionState the midpoint theorem.
- 7View SolutionThe sides of certain triangles are given below. Determine them are right triangles:
1.4cm, 4.8cm, 5cm. - 8In a $\triangle\text{ABC},\text{M}$ and N are points on the sides AB and AC respectively such that BM || BC.View Solution
- 9The corresponding sides of two similar triangles are in the ratio $2 : 3$. If the area of the smaller triangle is $48\ cm^2$, find the area of the larger triangle.View Solution
- 10In $\triangle\text{ABC},\text{AB}=\text{AC}.$ Side BC is produced to D. prove thatView Solution
$(\text{AD}^2-\text{AC}^2)=\text{BD}.\text{CD}$