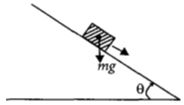
(a) Retardation in upward motion \( = g(\sin \theta + \mu \cos \theta )\)
\(\therefore \) Force required just to move up \({F_{up}} = mg(\sin \theta + \mu \cos \theta )\)
Similarly for down ward motion a \( = g(\sin \theta - \mu \cos \theta )\)
\(\therefore \) Force required just to prevent the body sliding down \({F_{dn}} = mg(\sin \theta - \mu \cos \theta )\)
According to problem \({F_{up}} = 2{F_{dn}}\)
\(⇒\) \(mg(\sin \theta + \mu \cos \theta ) = 2mg(\sin \theta - \mu \cos \theta )\)
\(⇒\) \(\sin \theta + \mu \;\cos \theta = 2\sin \theta - 2\mu \;\cos \theta \)
\(⇒\) \(3\mu \cos \theta = \sin \theta \)
\(⇒\) \(\tan \theta = 3\mu \)
\(⇒\) \(\theta = {\tan ^{ - 1}}(3\mu ) = {\tan ^{ - 1}}(3 \times 0.25) = {\tan ^{ - 1}}(0.75)\)\( = 36.8^\circ \)
Download our appand get started for free
Similar Questions
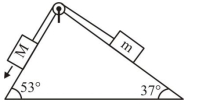
- 1આક્રૂતિમાં દર્શાવ્યા પ્રમાણે બે ઢોળાવાળા સમતલો ધરાવતા એક બ્લોકની ઢોળાવ વાળી સપાટી પર $M$ અને $m$ દળ ધરાવતા બે બ્લોકને ગોઈવી તેમને પુલ્લી પરથી પસાર થતી હલકી દોરી વડે બાંધેલ છે. અહી પુલ્લીઓ આદર્શ છે. ઢોળાવના સમતલ અને બ્લોક વરચે ઘર્ષાણ $0.25$ છે. જો $M=10 \mathrm{~kg}$ દળનો બ્લોક નીચે તરફ $2 \mathrm{~m} / \mathrm{s}^2$ ના પ્રવેગથી સરક્તો હોય તો $m$ નું મૂલ્ય.......View Solution
$\left(\mathrm{g}=10 \mathrm{~m} / \mathrm{s}^2\right.$ અને $\left.\tan 37^{\circ}=3 / 4\right)$
- 2View Solutionસમક્ષિતિજ રસ્તા પર થતી કારની પ્રવેગી ગતિ શાને આભારી છે
- 3$30^{\circ}$ ના ઘર્ષણરહિત ઢાળ પરથી સ્થિર સ્થિતિમાંથી એક પદાર્થ નીચે તરફ સરકવાનું શરૂ કરે છે, તેને નીચે આવતા $T$ સમય લાગે છે. જ્યારે સમાન પદાર્થ સમાન ખૂણો ધરાવતા ખરબચડા ઢાળ પરથી સ્થિર સ્થિતિમાંથી મુક્ત કરવામાં આવે ત્યારે તેને સમાન અંતર કાપતા $\alpha {T}$ જેટલો સમય લાગે છે. જ્યાં $\alpha$ એ $1$ કરતાં મોટો અચળાંક છે. પદાર્થ અને ખરબચડી સાપતિ વચ્ચેનો ઘર્ષણાંક $\frac{1}{\sqrt{{x}}}\left(\frac{\alpha^{2}-1}{\alpha^{2}}\right)$ છે, જ્યાં $x$ કેટલો હશે?View Solution
- 4$30^o$ ખૂણાવાળા ઢાળ પર $ 5\, kg$ નો બ્લોક મૂકતાં તે અચળ વેગથી ગતિની શરૂઆત કરતો હોય,તો ગતિક ઘર્ષણાંક કેટલો થાય?View Solution
- 5બે પાટિયાની રચનામાં તેનો એક છેડો ધીરે ધીરે બીજા છેડાની સાપેક્ષે ઊંચો થાય છે. જેના પર બોકસ મૂકેલ છે. જયારે આ પાટિયું સમક્ષિતિજ સાથે $30^o $ નો ખૂણો બનાવે છે,ત્યારે બોકસ નીચે તરફ સરકવાનું શરૂ કરે છે અને $4$ સેકન્ડમાં $4\; m$ અંતર કાપે છે.તો બોકસ અને પાટિયા વચ્ચે સ્થિત ઘર્ષણાંક અને ગતિક ઘર્ષણાંકના મૂલ્યો અનુક્રમે કેટલા હશે?View Solution
- 6એક ગ્રામોફોન રેકૉર્ડ $\omega$ જેટલા કોણીય વેગથી ભ્રમણ કરે છે. આ રેકૉર્ડના કેન્દ્રથી $r$ અંતરે એક સિક્કો મૂકેલો છે. સ્થિત-ઘર્ષણાંકનું મૂલ્ય છે. સિક્કો એ રેકૉર્ડની સાથે ભ્રમણ કરશે જો .......View Solution
- 7$50\;m$ ત્રિજયા ધરાવતા પથ પર $ 500 \;kg$ ની કાર $36\;km/hr$ ની ઝડપથી વળાંક લે છે. કેન્દ્રગામી બળ .......... $N$ થાય.View Solution
- 8$W$ દળની એક કાર $1\,Km$ સુધી $100\,m$ ચઢાણવાળા અને કાર પર $\frac {W}{20}$ જેટલું અચળ ઘર્ષણબળ લગાડતા રોડ પર છે. ચઢાણ પર $10\,ms^{-1}$ ઝડપથી ચડવા માટે કાર ને $P$ જેટલા પાવરની જરૂર પડે છે. જો તેને $v$ વેગથી નીચે ઉતારવા માટે $\frac {P}{2}$ જેટલા પાવરની જરૂર પડતી હોય તો $v$ નું મૂલ્ય ........ $ms^{-1}$ હશે.View Solution
- 9રફ સપાટી પર પડેલ $2\, kg $ ના બ્લોકનો વેગ $10\, m/s$ છે.જો ઘર્ષણાંક $0.2$ હોય,તો બ્લોક સ્થિર થાય ત્યાં સુધીમાં ....... $m$ અંતર કાપ્શે.View Solution
- 10સિમેન્ટ, પત્થર અને રેતી ને ભ્રમણ કરતાં નળાકારીય ડ્રમ માં મિશ્ર કરવાથી કોંક્રિટ મિશ્રણ બને છે. જો ડ્રમ ખૂબ જ ઝડપથી ભ્રમણ કરે તો તેમાની સામગ્રી દીવાલ સાથે ચોંટી જાય છે અને સામગ્રી નું યોગ્ય મિશ્રણ બનતું નથી. તો યોગ્ય મિશ્રણ બનાવવા માટે ડ્રમ ની મહત્તમ ભ્રમણ ઝડપ કેટલી હોવી જોઈએ? (ડ્રમની ત્રિજ્યા $1.25\, m$ અને ધરી સમક્ષિતિજ ધારો)View Solution
