ધારો કે એક નક્કર ગોળાની ત્રિજ્યા $R$ અને તેના પરનો વિદ્યુતભાર $Q$ છે. આ ગોળાનું વિદ્યુત ઘનતા વિતરણ $\rho( r )=\frac{ Q }{\pi R ^{4}} \cdot r$ સૂત્ર વડે અપાય છે. આ ગોળાની અંદર ગોળાના કેન્દ્રથી $r _{1}$ અંતરે આવેલા બિંદુ $P$ આગળ વિદ્યુતક્ષેત્રનું મૂલ્ય કેટલું થાય?
AIEEE 2009, Diffcult
d
Let us consider a spherical shell of thickness \(d x\) andradius \(x\).
Let us consider a spherical shell of thickness \(d x\) andradius \(x\).
The volume of this spherical shell \(=4 \pi r^{2} d r\).
The charge enclosed within shell
\(=\frac{Q r}{\pi R^{4}}\left[4 \pi r^{2} d r\right]\)
The charge enclosed in a sphere of radius \(r_{1}\) is
\(=\frac{4 Q}{R^{4}} \int_{0}^{r_{1}} r^{3} d r=\frac{4 Q}{R^{4}}\left[\frac{r^{4}}{4}\right]_{0}^{r}=\frac{Q}{R^{4}} r_{1}^{4}\)
\(\therefore \) The electric field at point \(p\) inside the sphere at a distance \(r_{1}\) from the centre of the sphere is
\(E=\frac{1}{4 \pi \epsilon_{0}}-\frac{\left[\frac{Q}{R^{4}} r_{1}^{4}\right]}{r_{1}^{2}}=\frac{1}{4 \pi \epsilon_{0}} \frac{Q}{R^{4}} r^{2}\)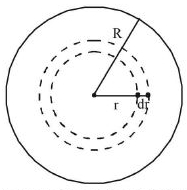
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1અનુક્રમે, $+ \sigma$ અને $+ \lambda$ વિદ્યુતભાર ધનતા ધરાવતા એક અનંત પૃષ્ઠ વિદ્યુતભાર અને અનંત રેખીય વિદ્યુતભારને, એકબીજાને સમાંતર $5\,m$ અંતરે રાખવામાં આવે છે. બિંદુ $P$ અને $Q$ એ રેખીય વિદ્યુતભારથી લંબઅંતરે પૃષ્ઠ તરફ અનુક્રમે $\frac{3}{\pi}\, m$ અને $\frac{4}{\pi}\,m$ અંતરે રહેલા બિંદુ છે. બિંદ્દુ $P$ અને $Q$ આગળ પરિણામી વિદ્યુતક્ષેત્ર ના મૂલ્યો અનુક્રમે $E_P$ અને $E _Q$ છે. જો $2|\sigma|=|\lambda|$ હોય, તો $\frac{E_P}{E_Q}=\frac{4}{a}$ મળે છે. $a$ નું મૂલ્ય ....... થશે.View Solution
- 2દરેક $m$ જેટલું દળ અને $q$ જેટલો વિદ્યુતભાર ધરાવતા બે એકસમાન ટેનિસ બોલને $l$ લંબાઈની દોરી વડે જડિત બિંદુથી લટકવવામાં આવેલ છે. જ્યારે શિરોલંબ સાથે દરેક દોરી નાનો કોણ $\theta$ રચતી હોય તો ત્યારે સંતુલન સ્થિતિમાં અંતર .......... હશે?View Solution
- 3જ્યારે ઇલેક્ટ્રોન અને પ્રોટોન $1.6 \;\mathring A$ અંતરે દૂર હોય ત્યારે તેમની વચ્ચેના આકર્ષણના લીધે ઇલેક્ટ્રોનનો પ્રવેગ ................... થાય $\left(m_{e} \simeq 9 \times 10^{-31} kg , e=1.6 \times 10^{-19} C \right)$View Solution
(Take $\frac{1}{4 \pi \varepsilon_{0}}=9 \times 10^{9} Nm ^{2} C ^{-2}$ )
- 4એક અનંત લંબાઈનો રેખીય વિદ્યુતભાર $2 \,cm$ અંતરે $9 \times 10^4 \;N/C$ વિદ્યુતક્ષેત્ર ઉત્પન્ન કરે છે. રેખીય વિદ્યુતભાર ઘનતા ($\mu C / m$ માં) ગણો.View Solution
- 5View Solutionસમાંગ વિદ્યુતક્ષેત્રમાં મૂકેલ વિદ્યુત ડાયપોલ કઈ સ્થિતિમાં બળયુગ્મની મહત્તમ ચાકમાત્રા અનુભવે છે ?
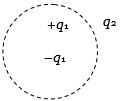
- 6View Solutionઆપેલ ગોળીય પૃષ્ઠમાંથી પસાર થતું વિદ્યુતક્ષેત્રના ફલ્કસ ગણતરી કરવા માટે લીધેલ વિદ્યુતક્ષેત્ર કયાં વિદ્યુતભારોના કારણે ઉત્પન્ન થશે?
- 7$10\,cm$ બાજુવાળા સમબાજુ ત્રિકોણ $ABC$ ના શિરોબિંદુ પર અનુક્રમે $1\,\mu C$ , $-1\,\mu C$ અને $2\,\mu C$ વિદ્યુતભાર મૂકતાં $C$ પર રહેલ વિદ્યુતભાર પર કેટલા .....$N$ બળ લાગે?View Solution
- 8$Q$ જેટલો વિદ્યુતભાર ધરાવતા બે બિંદુવત્ત વીજભારોને $d$ જેટલા અંતરે રાખવામાં આવ્યા છે. $q$ જેટલા બિંદુવત્ત ત્રીજા વિદ્યુતભારને લંબ દ્વિભાજક પર મધ્ય બિંદુ થી $x$ અંતરે છે $q$ પર મહત્તમ કુલંબબળ અનુભવે તે $x$ નું મૂલ્ય ............ હશે.View Solution
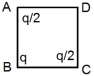
- 9$'a'$ બાજુ ધરાવતા ચોરસના ખૂણા (શિરોબિંદુ) $A, B$ અને $C$ ઉપર ત્રણ વિદ્યુતભારો $q/2, q$ અને $q/2$ મૂકેલા છે. (આકૃતિ જુઓ) બાકી રહેલા શિરોબિંદુ $D$ ઉપર વિદ્યુતક્ષેત્ર તીવ્રતાનું મૂલ્ય ........ હશે.View Solution
- 10$\rho (r) = \frac{A}{{{r^2}}}{e^{ - 2r/a}}$ જ્યાં $A$ અને $a$ અચળાંકો છે, જેટલી કદ વિદ્યુતભાર ઘનતા ધરાવતા $R$ ત્રિજ્યાના ગોળામાં વિદ્યુત ભારનું વિતરણ થયેલ છે. જો $Q$ એ આ વિતરણનો કુલ વિધુતભાર હોય તો ત્રિજ્યા $R$ કેટલી હશે.View Solution
