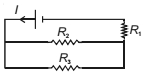
દર્શાવેલ પરિપથના સંદર્ભમાં લઈ.જો $R_1$ માં વ્યય થતો પાવર $P$ હોય. તો, પરિપથમાં થતો કુલ પાવર .......... $P$ હોઈ શકે આપેલ છે કે $R_2=4 R_1$ અને $R_3=12 R_1$ છે.
Medium
Download our app for free and get started
a
(a)
(a)
\(\frac{E}{16 R} R_3=12 R_1\)
\(R_{\text {net }}=4 R_1\)
\(i=\frac{E}{4 R_1}\)
\(P=\frac{E^2 R_1}{16 R_1^2}=\frac{E^2}{16 R_1}\)
\(P_2=\frac{9 E^2}{256 R_1{ }^2} \cdot 4 R_1=\frac{9 P}{4}\)
\(P_3=\frac{E^2}{256 R_1{ }^2} \cdot 12 R_1=\frac{3 E^2}{64 R_1}=\frac{3 P}{4}\)
\(P+\frac{9 P}{4}+\frac{3 P}{4}=\frac{16 P}{4}=4P\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
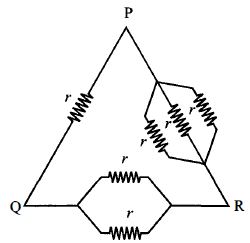
- 1View Solutionછ સમાન અવરોધને પરિપથમાં દર્શાવ્યા પ્રમાણે ગોઠવેલા છે. તો કયા બે બિંદુ વચ્ચેનો સમતુલ્ય અવરોધ મહત્તમ હશે?
- 2View Solutionજ્યારે ઇલેક્ટ્રીક હીટરને ચાલુ કરવામાં આવે ત્યારે સમય સાથે તેમાંથી વહેતા પ્રવાહને આકૃતિમાં દર્શાવેલ છે. તાપમાન સાથે અવરોધમાં થતા ફેરફારને ધ્યાનમાં લેતા નીચેનામાંથી કયો આલેખ સાચો છે ?
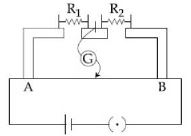
- 3આકૃતિમાં બતાવેલ મીટરબ્રીજનાં પ્રયોગની ગોઠવણમાં બિંદુ $A$ થી $40\, cm$ ના અંતરે તટસ્થ બિંદુ મળે છે. હવે જો $10\,\Omega$ ના અવરોધને $R_1$ સાથે શ્રેણીમાં જોડવામાં આવે, તો તટસ્થ બિંદુ $10\, cm$ જેટલું ખસે છે. હવે જો તટસ્થ બિંદુને પાછું તેની પ્રારંભિક સ્થિતિમાં લાવવુ હોય તો અવરોધ $(R_1 +10)\,\Omega$ ને સમાંતર કેટલા ................ $\Omega$ અવરોધ જોડવો પડે ?View Solution
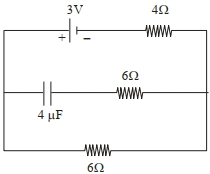
- 4નીચે આપેલા જાળતંત્ર માટે, સ્થાયી અવસ્થા માટે સંગ્રહાકમાં સંધારક સંગ્રહીત થતી વીજભાર .............. $\mu C$ હશે.View Solution
- 5એક તારમાંથી વહેતો વિધુતપ્રવાહ સમય સાથે $I = 3t^2 + 2t + 5$ સૂત્ર પ્રમાણે બદલાય છે, તો તારના કોઇ આડછેદમાંથી $t = 0$ થી $t = 2$ સેકન્ડના ગાળામાં પસાર થતો વિધુતભાર ........... $C$ થાય.View Solution
- 6બે એકસમાન પરિમાણ ધરાવતા ધાત્વીય તારોને શ્રેણીમાં જોડવામાં આવેલા છે. જે $\sigma_1$ અને $\sigma_2$ એ આ તારોની અનુક્રમે વાહકતા હોય, તો આ સંયોજનની અસરકારક વાહકતા $..........$ થશે.View Solution
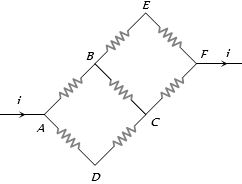
- 7નીચેના પરીપથમાં દરેક અવરોધનું મૂલ્ય $10\, \Omega$ ની હોય તો $AD$ માંથી વહેતો પ્રવાહ.... હશે.View Solution
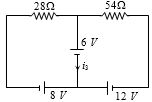
- 8આપેલ પરિપથમા $ i_3 $ નું મૂલ્ય કેટલું થાય?View Solution
- 9‘ $l$ ' લંબાઈના અને $100 \Omega$ અવરોધ ધરાવતા એક તારને $10$ સમાન ભાગોમાં વહેંચવામાં આવે છે. પ્રથમ $5$ ભાગોને શ્રેણીમાં જ્યારે બાકીના $5$ ભાગોને સમાંતરમાં જોડવામાં આવે છે. આ બંને સંયોજનોને ફરી વાર શ્રેણીમાં જોડવામાં આવે છે. અંતિમ સંયોજનનો અવરોધ. . . . . . . . . થશે.View Solution
- 10$1000 \;\Omega$ માં સુવાહકને $10\,V$ વિદ્યુતસ્થિતિમાનનો તફાવત આપવામાં આવે છે. તો $300\,s$ માં સુવાહકમાંથી પસાર થતાં ઈલેક્ટ્રોનની સંખ્યા કેટલી હશે?View Solution