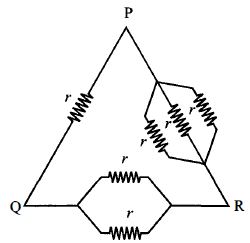
છ સમાન અવરોધને પરિપથમાં દર્શાવ્યા પ્રમાણે ગોઠવેલા છે. તો કયા બે બિંદુ વચ્ચેનો સમતુલ્ય અવરોધ મહત્તમ હશે?

JEE MAIN 2013, Diffcult
b
Resistance between \(\mathrm{P\,and\,} \mathrm{Q}\)
Resistance between \(\mathrm{P\,and\,} \mathrm{Q}\)
\(r_{P Q}=r_{11}\left(\frac{r}{3}+\frac{r}{2}\right)=\frac{r \times \frac{5}{6} r}{r+\frac{5}{6} r}=\frac{5}{11} r\)
Resistance between \(Q\) and \(R\)
\(\mathrm{r}_{\mathrm{QR}}=\frac{\mathrm{r}}{2} 11\left(\mathrm{r}+\frac{\mathrm{r}}{3}\right)=\frac{\frac{\mathrm{r}}{2} \times \frac{4}{3} \mathrm{r}}{\frac{\mathrm{r}}{2}+\frac{4}{3} \mathrm{r}}=\frac{4}{11} \mathrm{r}\)
Resistance between \(\mathrm{P}\) and \(\mathrm{R}\)
\({{\rm{r}}_{{\rm{PR}}}} = \frac{{\rm{r}}}{3}11\left( {\frac{{\rm{r}}}{2} + {\rm{r}}} \right) = \frac{{\frac{{\rm{r}}}{3} \times \frac{3}{2}{\rm{r}}}}{{\frac{{\rm{r}}}{3} + \frac{3}{2}{\rm{r}}}} = \frac{3}{{11}}{\rm{r}}\)
Hence, it is clear that \(\mathrm{r}_{\mathrm{PQ}}\) is maximum
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
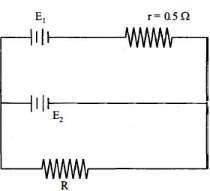
- 1$r = 0.5\,\Omega $ આંતરિક અવરોધ અને $ E_1 = 100\,V\;\;emf$ ધરાવતા $dc$ સ્ત્રોત સાથે $E_2 = 90\,V\;\;emf$ ધરાવતી બેટરી અને બાહ્ય અવરોધ $R$ ને પરિપથમાં દર્શાવ્યા પ્રમાણે જોડેલ છે $R$ નું મૂલ્ય કેટલા ................... $\Omega $ હોવું જોઈએ કે જેથી બેટરીમાંથી પ્રવાહ પસાર થાય નહીં?View Solution
- 2$12\, ohm$ અવરોધ ધરાવતા તારને વાળીને સમબાજુ ત્રિકોણ બનાવવામાં આવે તો બે ખૂણા વચ્ચેનો સમતુલ્ય અવરોધ કેટલો થાય?View Solution
- 3$10 \mathrm{~cm}$ લંબાઈ અને $\sqrt{7} \times 10^{-4} \mathrm{~m}$ ત્રિજ્યા ના તારને મીટર બ્રીજના જમણા ગેપમાં જોડેલ છે.જ્યારે ડાબા ગેપમાં અવરોધ પેટી વડે $4.5 \Omega$ નો અવરોધ જોડવામાં આવે ત્યારે ડાબા છેડેથી $60 \mathrm{~cm}$ આગળ તટસ્થબિંદૂ (સંતુલન લંબાઈ) મળે છે.જો તારની અવરોધકતા $\mathrm{R} \times 10^{-7} \Omega \mathrm{m}$ હોય તો $\mathrm{R}$ નું મૂલ્ય_____છે.View Solution
- 4$ 220\, V$ અને $800\,W$ ઇલેકટ્રીક સગડીને અને $220 \,V$ અને $100\,W$ ના ત્રણ લેમ્પને સમાંતરમાં $220\,V$ ના સપ્લાય સાથે જેાડતા કેટલા ................ $ampere$ પ્રવાહનું વહન થાય?View Solution
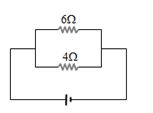
- 5આકૃતિમાં દર્શાવ્યા મુજબ $6\,\Omega$ અવરોધમાં ઉત્પન્ન થતો પાવર $6\ watt$ છે. તો $4\,\Omega$ અવરોધમાં ઉત્પન્ન થતો પાવર .... હશે.View Solution
- 6એક કોષ $2\, \Omega$ ના અવરોધમાંથી $0.9\,\ A$ પ્રવાહ અને $7\,\Omega$ ના અવરોધમાંથી $0.3\,\ A$ પ્રવાહ પસાર કરે છે. તો કોષનો આંતરિક અવરોધ .............. $\Omega$ છે.View Solution
- 7$60\,W,\;200\;V$ ની રેટિંગ ધરાવતા ત્રણ બલ્બને શ્રેણીમાં જોડીને તેને $200\;V$ ના સ્ત્રોત સાથે જોડવામાં આવે છે. આ ત્રણ બલ્બ દ્વારા વપરાતો પાવર કેટલા $W$ નો હશે?View Solution
- 8બે સમાન $500\, W$ અને $220 \,V$ ના બલ્બને $110\, V$ સાથે શ્નેણીમાં લગાવતા દરેક બલ્બમાં કેટલો પાવર વપરાય?View Solution
- 9આઠ સમાન કોષો કે જે દરેક સ્થિતિમાન $E$ અને આંતરિક અવરોધ $r$ ધરાવે છે. જે શ્રેણીમાં જોડાઈને બંધ પરિપથ રચે છે. $2$ કોષોના છેડે એક આદર્શ વોલ્ટમીટર જોડેલું છે જે ........ $E$ અવલોકન બતાવશે.View Solution
- 10$2\, V$ $emf$ અને $5\,Ω$ અવરોધ ધરાવતા કોષને $1000\, cm$ લંબાઇ અને $15\,Ω$ અવરોધ ધરાવતા તાર સાથે જોડવામાં આવતાં વિદ્યુતસ્થિતિમાન પ્રચલન કેટલું થાય?View Solution
