એક $2 \,kg$ દળનાં કણની સ્થિતિ ઊર્જા $(PE)$ એ વાળા $x$-અક્ષ $U(X)=\left(\frac{x^3}{3}-\frac{x^2}{2}\right)\, J$ વડે આપેલ છે. કણની કુલ યાત્રિક ઊર્જા $4 \,J$ છે. તો મહતમ ઝડપ $\left( ms ^{-1}\right.$ માં) કેટલી હશે?
Diffcult
d
(d)
(d)
\(U(x)=\frac{x^3}{3}-\frac{x^2}{2} \ldots (1)\)
\(F=\frac{-d U}{d x}=\frac{3 x^2}{3}-\frac{2 x}{2}=0\)
\(x^2-x=0\)
\(\Rightarrow x=1,0\)
Potential energy is minimum at \(x=1 m\) and the value of this minimum \(P.E.\) will be \(U=\frac{-1}{6} J\) (Putting \(x=1\) in \((1)\))
Now, \(E=U+K\)
Kinetic energy will be maximum, when potential energy will be minimum
\(4=\frac{-1}{6}+K\)
\(K=\frac{25}{6}\)
\(\frac{1}{2} m v_m^2=\frac{25}{6}\)
\(v_m=\frac{5}{\sqrt{6}}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
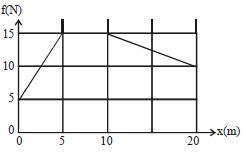
- 1આકૃતિમાં ગતિમાન કણ માટે ઘર્ષણબળ વિરુદ્ધ સ્થાનાંતર નો આલેખ દર્શાવેલો છે. $s = 0$ થી $20\, m$ સુધી ની ગતિ દરમ્યાન ગતિઉર્જામાં થયેલ ઘટાડો કેટલા .....$J$ હશે?View Solution
- 2એક $m$ દળવાળી કાર એ એવું એન્જિન ધરાવે છે જે $P$ જેટલો પાવર પૂરો પાડી શકે છે. તો કારએ કેટલાં ન્યૂનતમ સમયમાં સ્થિર સ્થિતિમાંથી $v$ જેટલી ઝડપ સુધી પ્રવેગિત થઈ શકે છે તે...View Solution
- 3$1$ $kg$ દળ ધરાવતા એક કણ પર $F=6t$ નું સમય આધારિત બળ લાગે છે.જો કણ સ્થિર સ્થિતિમાંથી શરૂ કરે તો પ્રથમ $1$ $sec.$ માં બળ વડે થતું કાર્ય ............... $\mathrm{J}$ હશે.View Solution
- 4$5 \times 10^{3} \,kg$નો પદાર્થ $2\, m / s$ના વેગથી ગતિ કરીને $15 \times 10^{3} \,kg$ દળના સ્થિર પદાર્થ સાથે અથડાઈને ચોંટી જાય તો તંત્રમાં ગુમાવેલી ગતિ ઊર્જા શોધો. ($KJ$ માં)View Solution
- 5View Solutionકોની હાજરીમાં કાર્ય-ઊર્જા પ્રમેય પ્રમાણભૂત (માન્ય) છે?
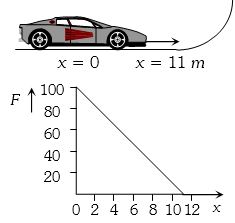
- 6$5 kg$ ની રમકડાની કારનો બળ વિરુધ્ધ સ્થાનાંતરનો આલેખ આપેલ છે.તો તે કેટલી મહત્તમ ઊંચાઇ પ્રાપ્ત કરશે?View Solution
- 7View Solutionવિધાન: સ્પ્રિંગની સ્થિતિઉર્જા વિરુદ્ધ સ્પ્રિંગનું ખેંચાણ અથવા દબાણ નો આલેખ સુરેખા મળે.
કારણ: ખેંચાયેલી કે દબાયેલી સ્પ્રિંગની સ્થિતિઉર્જા એ ખેંચાણ કે દબાણ ના વર્ગના સમપ્રમાણ માં હોય.
- 8$2000 kg$ ની લિફટ ભોંયરામાંથી સ્થિર સ્થિતિમાંથી $25m$ ઉંચાઈએ ચોથા માળે જાય છે. જ્યારે તે ચોથો માળેથી પસાર થાય ત્યારે $3 ms^{-1}$ ની ઝડપ છે. અહી અચળ ઘર્ષણ બળ $500 N $ લાગે છે. લિફટની યાંત્રિકને વડે થતું કાર્ય ....... $kJ$ ગણો.View Solution
- 9એક અવકાશયાન કે જેનુ દળ $M$ છે. તે $V$ જેટલા વેગથી ગતિ કરે છે અને અચાનક બે ભાગમાં ફાટે છે. તેનો એક $m$ દળનો ભાગ સ્થિર લઇ જાય છે. ત્યારે બીજા ભાગનો વેગ કેટલો હશે?View Solution
- 10$m_1$ દળનો એક કણ $m_2$ દળના સ્થિર સ્થિતિએ રહેલા બીજાકણ સાથે સંપૂર્ણ અસ્થિતિ સ્થાપક હેડ ઓન સંઘાત અનુભવે છે. ($m_2$ > $m_1$). આ સંઘાતમાં ઘર્ષણની ગતિઊર્જા કેટલા મૂલ્યની ઉષ્માઊર્જામાં રૂપાંતરણ પામશે?View Solution
