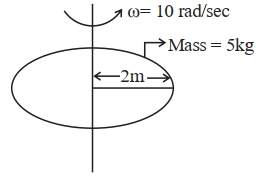
એક $5 \mathrm{~kg}$ દળ, $2 \mathrm{~m}$ ત્રિજ્યા અને તેના પરિભ્રમણ સમતલને લંબ અક્ષને અનુરુપ કોણીય વેગ $10 \mathrm{rad} / \mathrm{sec}$ ધરાવતી એક તક્તિ ધ્યાનમાં લો. આ જ અક્ષની દિશામાં બીજી એક સમાન તક્તિને હળવેકથી ભ્રમણ કરતી તક્તિ ઉપર મૂકવામાં આવે છે. બંને તક્તિઓ સરક્યા સિવાય એકબીજા સાથે પરિભ્રમણ કરે તે માટે વિખેરીત થતી ઊર્જા_____________$j$ છે .

JEE MAIN 2024, Diffcult
d
\( \vec{L}_i=I \omega_i=\frac{M R^2}{2} \cdot \omega=100 \mathrm{kgm}^2 / \mathrm{s} \)
\( \vec{L}_i=I \omega_i=\frac{M R^2}{2} \cdot \omega=100 \mathrm{kgm}^2 / \mathrm{s} \)
\( E_i=\frac{1}{2} \cdot \frac{M R^2}{2} \cdot \omega^2=500 \mathrm{~J} \)
\( \vec{L}_i=\vec{L}_f \Rightarrow 100=2 I \omega_f \)
\( \omega_{\mathrm{f}}=5 \mathrm{rad} / \mathrm{sec} \)
\( E_f=2 \times \frac{1}{2} \cdot \frac{5(2)^2}{2} \cdot(5)^2=250 \mathrm{~J} \)
\( \Delta E=250 \mathrm{~J}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
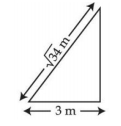
- 1$\sqrt{34} \,m$ લાંબી અને $10 \,kg$ વજન ધરાવતી એક સીડી (નીસરણી) ધર્ષણરહિત દિવાલ પર ટેક્વેલ છે. આકૃતિમાં દર્શાવ્યા પ્રમાણે તેના પગ (નીચેનો છેડો) દિવાલથી $3 \,m$ અંતરે રાખેલ છે. જો $F _{f}$ અને $F _{ w }$ એ અનુક્રમે ભોંયતળિયા અને દિવાલ દ્વારા લાગતું લંબબળ હોય તો ગુણોત્તર $F _{ w } / F _{f}$ ............ થશે.View Solution
$\left(g=10 \,m / s ^{2}\right.$ નો ઉપયોગ કરો.)
- 2એક પૈડાની તેની શિરોલંબ અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા $2 \;kg \,m ^{2}$ છે, જે આ અક્ષને અનુલક્ષીને $60 \;rpm$ ના દરથી ભ્રમણ કરે છે. આ પૈડાને $1$ મિનિટમાં સ્થિર કરવા માટે કેટલુ ટોર્ક લગાવવું પડે?View Solution
- 3$1\,kg$ દળની વસ્તુનો સ્થાન સદિશ $\overrightarrow{ r }=(3 \hat{ i }-\hat{ j }) \,m$ અને તેનો વેગ $\overrightarrow{ v }=(3 \hat{ j }+\hat{ k }) \,ms ^{-1}$ છે. કોણીય વેગમાનનું મૂલ્ય $\sqrt{x} \,Nm$ મળે છે તો $x$ નું મૂલ્ય ............ હશે.View Solution
- 4એક ઘન ગોળો ગબડતી ગતિમાં છે.ગબડતિ ગતિ (લોટણ ગતિ) માં પદાર્થ સ્થાનાંતરીત ગતિઊર્જા $(K_t) $ અને ભ્રમણીય ગતિઊર્જા $(K_r)$ એક સાથે ધરાવે છે.આ ગોળા માટે $ K_t: (K_t+ K_r)$ નો ગુણોત્તર છે.View Solution
- 5$3\ kg$ દળના દઢ પદાર્થને $ 2\ kg$ સાથે દળ રહિત સળિયા સાથે જોડેલો છે. $3\ kg$ દાળ ${{{\vec r}}_{\,{\text{1}}}}\, = \,\,(2\,\hat i\,\, + \,\,5\,\hat j)\,m$ પર અને ${\text{2}}\,{\text{kg}}$ દળ ${{{\vec r}}_{\,{\text{2}}}}\, = \,\,(4\,\hat i\,\, + \,\,2\,\hat j)\,m$ દળ પર રહેલા છે. સળિયાની લંબાઈ અને દ્રવ્યમાન કેન્દ્રના યામ શોધો.View Solution
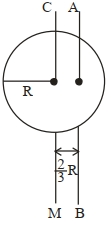
- 6એક વર્તુળાકાર તક્તિની, તક્તિના સમતલને લંબ અને કેન્દ્રમાંથી પસાર થતી અક્ષ $(CM)$ ને અનુલક્ષીને જડત્વની ચાકમાત્રા $I _{ CM }$ છે. $I _{ AB }$ એ સમતલને લંબ અને $CM$ અક્ષને સમાંતર, કેન્દ્રથી $\frac{2}{3} R$ અંતરે પસાર થતી અક્ષ $AB$ ને અનુરૂપ, જડત્વની યાકમાત્રા છે, જ્યાં $R$ એ તક્તિની ત્રિજ્યા છે. $I _{ AB }$ અને $I _{ CM }$ નો ગુણોત્તર $x : 9$ મળે છે. $x$ નું મૂલ્ય $........$ થશે.View Solution
- 7$M$ દળ અને $R$ ત્રિજ્યાના ઘન ગોળાની તેની અક્ષને અનુલક્ષીને ચક્રાવર્તન ત્રિજ્યા, અને તેટલા જ દળ અને ત્રિજ્યા ધરાવતા પાતળા પોલા ગોળાની, તેની અક્ષને અનુલક્ષીને ચક્રાવર્તન ત્રિજ્યાનો ગુણોત્તર $.........$ છે.View Solution
- 8નીચે આપેલા પદાર્થોને એક ઢાળ પર નીચેથી ઉપર તરફ (સરક્યાં વગર) ભ્રમણ કરવવામાં આવે છેView Solution
$(i)$ $R$ ત્રિજ્યાની રિંગ
$(ii)$ $\frac {R}{2}$ ત્રિજ્યાનો ઘન નળાકાર અને
$(iii)$ $\frac {R}{4}$ ત્રિજ્યાનો ઘન ગોળો
જો ઢાળના તળિયે બધાના દ્રવ્યમાન કેન્દ્રનો વેગ સમાન હોય તો તેમના દ્વારા પ્રાપ્ત થતી મહત્તમ ઊંચાઈનો ગુણોત્તર કેટલો થાય?
- 9એક કારનું વજન $1800\; kg$ છે. તેની આગળ અને પાછળની એક્સેલ્સ (ધરીઓ) વચ્ચેનું અંતર $1.8\; m$ છે. તેનું ગુરુત્વકેન્દ્ર આગળની એક્સલથી $1.05\; m$ પાછળ છે. સમતલ જમીન દ્વારા આગળના દરેક પૈડા (વ્હીલ) પર લાગતું બળ શોધો.View Solution
- 10કોઈ સમક્ષિતિજ સમતલ તેના કેન્દ્રમાથી પસાર થતી શિરોલંબ અક્ષને અનુલક્ષીને નિયમિત કોણીય વેગથી ભ્રમણ કરે છે. કોઈ ક્ષણે $m$ દળના ઘટ્ટ પ્રવાહીને તેના કેન્દ્ર પર પાડતા તે ફેલાઈને નીચે પડે છે. આ દરમિયાન તેનો કોણીય વેગમાં શું થશે?View Solution
