એક આદર્શ વાયુ નીચે દર્શાવેલ આકૃતિ મુજબ ચક્રીય પ્રક્રમ અનુભવે છે.

$\Delta {U_{BC}} = - 5\,kJ\,mo{l^{ - 1}},{q_{AB}} = 2\,kJ\,mo{l^{ - 1}}$

$\Delta {W_{AB}} = - 5\,kJ\,mo{l^{ - 1}},{W_{CA}} = 3\,kJ\,mo{l^{ - 1}}$

$CA$ પ્રક્રમ દરમિયાન પ્રણાલી દ્વારા શોષાતી ઉષ્મા ......$kJ\,mo{l^{ - 1}}$

Question

એક આદર્શ વાયુ નીચે દર્શાવેલ આકૃતિ મુજબ ચક્રીય પ્રક્રમ અનુભવે છે.

$\Delta {U_{BC}} = - 5\,kJ\,mo{l^{ - 1}},{q_{AB}} = 2\,kJ\,mo{l^{ - 1}}$

$\Delta {W_{AB}} = - 5\,kJ\,mo{l^{ - 1}},{W_{CA}} = 3\,kJ\,mo{l^{ - 1}}$

$CA$ પ્રક્રમ દરમિયાન પ્રણાલી દ્વારા શોષાતી ઉષ્મા ......$kJ\,mo{l^{ - 1}}$

JEE MAIN 2018, Diffcult

Download our app for free and get started

Solution

b
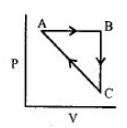
$\Delta {U_{AB}} = {q_{AB}} + {W_{AB}} = 2 + ( - 5) = - 3\,kJ/mol$

$\Delta {U_{BC}} = - 5\,kJ/mol$

For cyclic procrss, $\Delta U=0$

$\Delta {U_{AB}} + \Delta {U_{BC}} + \Delta {U_{CA}} = 0$

$\Delta {U_{CA}} = - \Delta {U_{AB}} - \Delta {U_{BC}}$

$\Delta {U_{CA}} = - ( - 3) - ( - 5) = 8\,kJ/mol$

$\Delta {U_{CA}} = {q_{CA}} + {W_{CA}}$

$8 = {q_{CA}} + 3$

${q_{CA}} = + 5\,kJ/mol$

Heat absorbed has positive sign.

Download our app
and get started for free