એક બીકરમાં $\rho \, kg / m^3$ ઘનતા, વિશિષ્ટ ઉષ્મા $S\, J / kg\,^oC$ અને શ્યાનતા $\eta $ વાળું પ્રવાહી ભરેલ છે, બીકર $h$ ઊંચાઈ સુધી ભરેલ છે. બીકરને ગરમ પ્લેટ પર મૂકતા તેમાં સંવહન દ્વારા એકમ ક્ષેત્રફળ દીઠ ઉષ્મા પ્રસરણ દર $(Q/A)$ ના અનુમાપન માટે એક વિદ્યાર્થી ધારે છે કે તે $\eta \;\left( {\frac{{S\Delta \theta }}{h}} \right)$ અને $\left( {\frac{1}{{\rho g}}} \right)$ પર આધારિત છે, જ્યા $\Delta \theta $ ($^oC$ માં) એ ઉપરના અને નીચેના ભાગના તાપમાનનો તફાવત છે. આ પરિસ્થિતિમાં $(Q / A)$ માટે નીચેનામાથી કયું સાચું છે?
JEE MAIN 2015, Diffcult
d
\(\begin{array}{l}
Let\,\frac{Q}{A} = {\eta ^a}{\left( {\frac{{S\Delta \theta }}{h}} \right)^b}{\left( {\frac{1}{{\rho g}}} \right)^c}\\
{\rm{Using}}\,{\rm{dimensional}}\,method\\
M{T^{ - 3}} = {\left[ {M{L^{ - 1}}{T^{ - 1}}} \right]^a}{\left[ {L{T^{ - 2}}} \right]^b}{\left[ {{M^{ - 1}}{L^2}{T^2}} \right]^c}\\
or,\,M{T^{ - 3}} = \left[ {{M^{a - c}}{L^{ - a + b + 2c}}{T^{ - a - 2b + 2c}}} \right]\\
Equating\,powers\,and\,solving\\
we\,get,a = 1,b = 1,c = 0\\
\therefore \frac{Q}{A} = \eta \frac{{S\Delta \theta }}{h}
\end{array}\)
\(\begin{array}{l}
Let\,\frac{Q}{A} = {\eta ^a}{\left( {\frac{{S\Delta \theta }}{h}} \right)^b}{\left( {\frac{1}{{\rho g}}} \right)^c}\\
{\rm{Using}}\,{\rm{dimensional}}\,method\\
M{T^{ - 3}} = {\left[ {M{L^{ - 1}}{T^{ - 1}}} \right]^a}{\left[ {L{T^{ - 2}}} \right]^b}{\left[ {{M^{ - 1}}{L^2}{T^2}} \right]^c}\\
or,\,M{T^{ - 3}} = \left[ {{M^{a - c}}{L^{ - a + b + 2c}}{T^{ - a - 2b + 2c}}} \right]\\
Equating\,powers\,and\,solving\\
we\,get,a = 1,b = 1,c = 0\\
\therefore \frac{Q}{A} = \eta \frac{{S\Delta \theta }}{h}
\end{array}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$m$ દળના પદાર્થને વહેતી નદી ખસેડે છે.તે નદીનો વેગ $V$, પાણીની ઘનતા $(\rho )$ અને ગુરુત્વપ્રવેગ $g$ પર આઘાર રાખે છે.તો $m \propto $View Solution
- 2View Solutionનીચેનામાંથી કયું સૂત્ર પારિમાણિક રીતે ખોટ્ટું છે?
- 3$M,L,T$ અને $C$ (કુલંબ) ના સ્વરૂપમાં ચુંબકીય ક્ષેત્રનું પારિમાણિક સૂત્ર શું થાય?View Solution
- 4View Solutionપૃથ્વીની સપાટી પર એકમ ક્ષેત્રફળ દીઠ એકમ સમયમાં મેળવાતી સુર્યની ઉર્જાને સોલર અચળાંક કહે છે. તો સોલર અચળાંકનું પરિમાણ શું થાય?
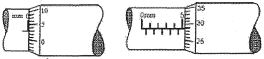
- 5સ્ક્રૂગેજની આકૃતિ આપેલ છે. આકૃતિ $(i)$ માં સ્ક્રૂગેજ જ્યારે બંધ કરેલ હોય ત્યારની શૂન્ય ત્રુટિ દર્શાવેલ છે. આકૃતિ $(ii)$ માં બોલ બેરિંગના વ્યાસ માપવા માટે લીધેળ અવલોકન માટેની સ્ક્રૂગેજની આકૃતિ છે. તો બોલ બેરિંગનો વ્યાસ ($mm$ માં) કેટલો હશે? વર્તુળાકાર સ્કેલમાં $50$ કાંપા છે.View Solution
- 6કોઈ સ્ટીલના દડાનો વ્યાસ વર્નિયર કેલિપર્સ વડે માપતા મુખ્ય સ્કેલ $(MS)$ પર $0. 1\,cm$ અને ગૌણ સ્કેલ $(VS)$ નો $10$ મો કાપો મુખ્ય સ્કેલના $9$ માં કાપા સાથે એકરૂપ થાય છે. દડા ના એવા ત્રણ માપન નીચે પ્રમાણે છે:View Solution
જો શૂન્યાંક ત્રુટિ $- 0.03\,cm$ હોય, તો સુધારેલો સરેરાશ વ્યાસ $........... cm$ થાય.ક્રમાંક મુખ્ય સ્કેલનું માપ $(cm)$ ગૌણ સ્કેલના કાપા $(1)$ $0.5$ $8$ $(2)$ $0.5$ $4$ $(3)$ $0.5$ $6$ - 7વાયુનું સમીકરણ $ \left( {P + \frac{a}{{{V^2}}}} \right)\,(V - b) = RT $ મુજબ આપવામાં આવે છે જ્યાં $P$ દબાણ, $V$ કદ, $T$ નિરપેક્ષ તાપમાન અને $a,b,R$ અચળાંક છે તો સમીકરણ માં $a$ નું પારિમાણીક સૂત્ર શું હશે?View Solution
- 8જો બળ $({F})$, લંબાઈ $({L})$ અને સમય $({T})$ ને મૂળભૂત રાશિ લેવામાં આવે છે. તો ધનતાનું પરિમાણ શું થાય?View Solution
- 9View Solutionનીચે પૈકી ઉર્જાનો એકમ કયો છે?
- 10આપેલ એક સ્ક્રૂગેજમાં વર્તુળાકાર સ્કેલ પર પિચ અને કાપાઓની સંખ્યા અનુક્રમે $ 0.5\,mm$ અને $100$ છે. જ્યારે આ સ્ક્રૂગેજ પૂર્ણતઃ કોઈપણ પદાર્થ વગર બંધ છે, ત્યારે વર્તુળાકાર માપપટ્ટીનું શૂન્ય સરેરાશ રેખાની $3$ કાપા નીચે છે. એક પાતળી તક્તિ માટે મુખ્ય માપપટ્ટી અને વર્તુળાકાર માપપટ્ટીના વાંચનો અનુક્રમે $5.5\, mm$ અને $48$ છે. આ તક્તિની જાડાઈ કેટલી હશે?View Solution
