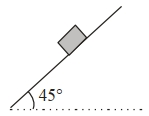
(a)
\(\sum F_y=0\)
\(\Rightarrow N =10 g \cos \theta / m _{ A }=10\,kg\)
\(\sum F_x=m_A \cdot a_A\)
\(\Rightarrow 10 g \cdot \sin \theta=10 . a _{ A }\)
\(\Rightarrow a_A=g \sin \theta---\) (i)
\(\sum F_y=0\)
\(N =20 g \cos \theta----\) (ii) \(/ m _{ B }=20\,kg\)
\(\sum F _{ x }= m _{ B } a _{ B }\)
\(\Rightarrow 20\, g \sin \theta- fk =20 a _{ B }\)
\(\Rightarrow 20\, g \sin \theta-\mu_{ k } \cdot 20 g \cos \theta=20 a _{ B } g\)
\(f _{ k }=\mu_{ k } \cdot N\)
\(=\mu_{ k } \cdot 20\, g \cos \theta\)
from \((ii)\)
\(\Rightarrow \sin \theta-\mu_{ k } \cdot \cos \theta=\frac{a_{ B }}{g}\)
\(\Rightarrow a _{ B }= g \left(\sin \theta- mu _{ k } \cos \theta\right)---\) (iii)
\((i) \div (iii):\)
\(\frac{a_A}{a_B}=\frac{g \sin \theta}{g\left(\sin \theta-\mu_k \cos \theta\right)}=\frac{\sin \theta}{\sin \theta\left(1-\mu_{ K } \cdot \cot \theta\right)}\)
\(\Rightarrow \frac{2}{1}=\frac{1}{1-\mu_{ k }} \Rightarrow\left(1-\mu_{ k }\right) 2=1\)
\(\theta=45^{\circ}\)
\(\cot 45^{\circ}=1\)
\(\Rightarrow 2-2 \mu_{ k }=1 \Rightarrow \mu_{ k }=0.5\)
Download our appand get started for free
Similar Questions
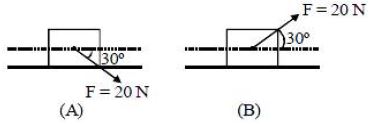
- 1$5\, kg$ ના બ્લોક ને, $(i)$ કિસ્સા $(A)$ મુજબ ધકેલવામાં અને $(ii)$ કિસ્સા $(B)$ મુજબ ખેચવામાં આવે છે,જ્યાં બળ $F = 20\, N$,સમક્ષિતિજ સાથે $30^o$ ના ખૂણે આકૃતિમાં દર્શાવ્યા મુજબ આપવામાં આવે છે. બ્લોક અને સપાટી વચ્ચેનો ઘર્ષણાંક $\mu = 0.2$ છે. કિસ્સા $(B)$ અને કિસ્સા $(A)$ ના પ્રવેગનો તફાવત ........ $ms^{-2}$ મળશે. $(g = 10\, ms^{-2})$View Solution
- 2$1000\; kg $ દળની કાર $90\; m$ ત્રિજયા ધરાવતા ઘર્ષણરહિત રોડ પર ગતિ કરે છે. જો ઢોળાવ $ 45^o $ નો હોય, તો કારની ઝડપ ($ms^{-1}$ માં) કેટલી હશે?View Solution
- 3View Solutionજયારે માણસ રફ સપાટી પર ચાલતો હોય તે સ્થિતિમાં નીચેનામાથી ક્યુ સાચું છે
- 4રફ સપાટી પર પડેલ $60\, kg $ ના બ્લોકને ગતિ માટે જરૂરી બળ આપવામાં આવે છે.બ્લોક ગતિમાં આવ્યા પછી પણ આ બળ લગાવવાનું શરૂ રાખવામાં આવે,તો ....... $m/{s^2}$ પ્રવેગ ઉત્પન્ન થશે. બ્લોક અને સપાટી વચ્ચેનો સ્થિત અને ગતિક ઘર્ષણાંક અનુક્રમે $0.5$ અને $0.4$ છેView Solution
- 5$2\, kg$ ના પદાર્થને $45^°$ ના રફ ઢાળ જેનો ઘર્ષણાંક $1.7$ પરથી નીચે આવતા પદાર્થ પર કેટલું ઘર્ષણબળ લાગતું હશે?View Solution
- 6View Solutionજ્યારે ઢાળ પર રહેલો પદાર્થ ગતિ ના કરે તો ઘર્ષણબળ ...
- 7કાર એક રોડ પર $10\, m/s$ ની અચળ ઝડપ થી લપસણા રોડ પર ગતિ કરે છે. ઘર્ષણાક $0.5$ હોય તો કાર ફેરવવા માટે ની રોડની ન્યૂનતમ ત્રિજ્યા (m)View Solution
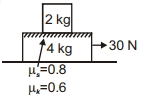
- 8આપેલી આકૃતિમાં બે બ્લોકનું તંત્ર દર્શાવે છે, $4 \,kg$ નો બ્લોક એ લીસી સમક્ષિતિજ સપાટી પર સ્થિર છે, $4 \,kg$ ની ઉપરની સપાટી ખરબચડી છે. $2 \,kg$ નો એક બ્લોક તેની ઉપરની સપાટી પર મૂકવામાં આવે છે. જ્યારે $4 \,kg$ દળને $30 \,N$ બળ દ્વારા ખેંચવામાં આવે છે, ત્યારે પૃથ્વીની સાપેક્ષે ઉપરની બ્લોકનો પ્રવેગ ............... $m / s ^2$ છેView Solution
- 9$0.5$ ઘર્ષણાંક ધરાવતા ઢાળ પર બ્લોક મૂકતાં લંબ બળ એ પરિણામી ઢાળને સમાંતર લાગતા બળ કરતાં બમણું છે,તો ઢાળનો ખૂણો ........ $^o$ હશે.View Solution
- 10આકૃતિમાં દર્શાવ્યા પ્રમાણે ઢળતા સમતલ પર ($45^{\circ}$ પર ઢળતા) બ્લોકને ધ્યાનમાં લો. જો ઢાળ પર ઉપરની તરફ ધકેલવા માટેનું બળ તેને સરકતો અટકાવવા માટેના બળ કરતાં બમણું હોય તો બ્લોક અને ઢાળના સમતલ વચ્યેનો ધર્ષણાંક $(\mu)$ બરાબર $.......$ હોય.View Solution