લિફ્ટમાં સ્પ્રિંગ બેલેન્સ પર $2\, kg$ નો દળ લટકાવેલ છે. હવે લિફ્ટ $2 \,m/sec^2$ ના પ્રવેગથી ઉપર તરફ ગતિ કરે, તો સ્પ્રિંગ બેલેન્સનું અવલોકન ....... $kg$ હશે.
Easy
Download our app for free and get started
d
(d) When lift moves upward then reading of the spring balance,
(d) When lift moves upward then reading of the spring balance,
\(R = m(g + a) = 2(g + g) = 4g\;N = 4\;kg\) [As \(a = g\)]
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
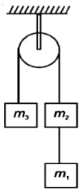
- 1$m_1=4 \,kg , m_2=2 \,kg , m_3=4 \,kg$ દળનો ત્રણ બ્લોકને લીસી દળરહિત ગરગડી પરથી આકૃતિમાં દર્શાવ્યા મુજબ પસાર કરેલી આદર્શ દોરીથી જોડેલ છે. તો બ્લોકનો પ્રવેગ ......... $m / s ^2$ હશે. $\left(g=10 \,m / s ^2\right)$View Solution
- 2$500\,g$ નું વજન ધરાવતો પદાર્થ $x-$અક્ષ પર એવી રીતે ગતિ કરે છે કે જેનો વેગ, સ્થાનાંતર $x$ સાથે $v=10 \sqrt{x}\,m / s$ ના સંબંધથી બદલાય છે. આ પદાર્થ પર લાગતું બળ .......... $N$ છે.View Solution
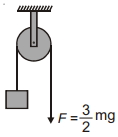
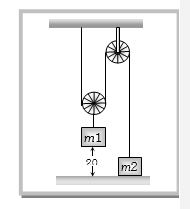
- 3આકૃતિમાં દર્શાવેલી ગોઠવણી માટે, $m$ દળ કેટલું પ્રવેગ સાથે ઉપર તરફ ગતિ કરશે ?(ગરગડી અને દોરી ઘર્ષણરહિત છે)View Solution
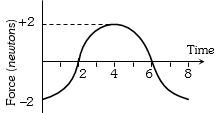
- 4કણનો બળ વિરુધ્ધ સમયનો આલેખ આપેલ છે. $0$ અને $ 8 sec $ વચ્ચે વેગમાનમાં કેટલો વધારો થશે?View Solution
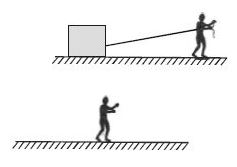
- 5View Solutionવિધાન: એક માણસ અને એક બ્લોક કોઈ લીસી સમક્ષિતિજ સપાટી પર સ્થિર છે. માણસ બ્લોક સાથે બાંધેલું દોરડું ખેંચે છે. પણ તે સમક્ષિતિજ સપાટી પણ ચાલી કરી શકતો નથી.
કારણ: ઘર્ષણ ની ગેરહાજરી ને લીધે સમક્ષિતિજ સપાટી પર ઉભેલો માણસ ચાલવાનું શરૂ કરી શકતો નથી.
- 6બંદુક દ્વારા ગોળી પર લાગતું બળ $F =\left(100-0.5 \times 10^{5} t \right) N$ છે.ગોળી $400 \,m / s$ નાં વેગથી બહાર આવે છે.જ્યારે ગોળી પર બળ શૂન્ય થાય. ત્યારે બળનો આઘાત ($N - s$ માં) કેટલો હશે?View Solution
- 7$2 \,kg$ દળનો કોઈ સ્થિર પદાર્થ $\vec{F}=\left(3 t^2 \hat{i}+4 \hat{j}\right) \,N$ બળની અસર હેઠળ તેના ઉગમબિંદુથી ગતિ કરવાનું શરૂ કરે છે. પદાર્થનો વેગ $t=2 \,s$ સમય પર .............. $m / s$ હશે.View Solution
- 8કોઈ $m$ દળના કણ પર પ્રયોગમુલક નિયમ પ્રમાણે બળ $F = \frac{R}{{{t^2}}}\,v(t)$ લગાવવામાં આવે છે. ગતિની શરુઆતની સ્થિર સ્થિતિ થી પ્રાયોગિક રીતે આ નિયમ ની કસોટી કરવી હોય તો તેના માટે ..... નો વક્ર દોરવો એ ઉત્તમ રસ્તો છે.View Solution
- 9જો $ m_1 = 4m_2$ છે . $m_1 $ નો પ્રવેગ $a$ છે. તો દોરીમાં તણાવ $T =$ ____View Solution
- 10$2\, kg$ દળ ધરાવતો પદાર્થ $(2 \hat{ i }+3 \hat{ j }+5 \hat{ k }) \,N$ બળની અસર હેઠળ ગતિ કરે છે. તે વિરામ સ્થિતિમાંથી શરૂ કરે છે. તે પ્રારંભમાં ઊગમબિંદુ આગળ હતો. $4$ સેકન્ડ બાદ, તેના નવા યામો $(8, b, 20)$ છે. $b$ નું મૂલ્ય ...... . (નજીકત્તમ પૂર્ણાંકમાં લખો)View Solution