c
ન્યુટન ના સૂત્ર પરથી \(({{\vec v}_2}-{{\vec v}_1})=e({{\vec u}_1}-{{\vec u}_2})\)

\({\text{v}}\,\, = \,\,\sqrt {{\text{2gh}}} \,\) અહી, \({{\vec v}_2}\, = \,\,0,\,\,{{\vec u}_2}\, = \,\,0\,\) (સ્થિર સ્થિતિ આગળ ની સપાટી )

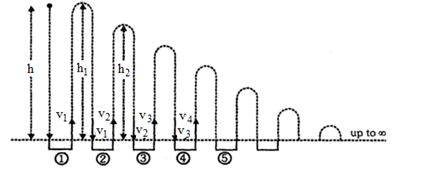
\('n '\) વાર પાછો ફર્યા પછી બોલ વડે હાંસલ થતી ઊંચાઈ :

\({v_1}\, = \,\,ev\,\,\,\, \Rightarrow \,\,\sqrt {2g{h_1}} \,\,\, = \,\,\,e\,\,\sqrt {2gh} \,\,\, \Rightarrow \,\,\,{h_1}\, = \,\,{e^2}h{v_2}\, = \,\,{e^2}v\)

\(\sqrt {2g{h_2}} \,\,\, = \,\,\,{e^2}\,\,\sqrt {2gh} \,\,\,\, \Rightarrow \,\,\,\,{h_2}\, = \,\,{e^4}h\)

તેવી જ રીતે, \({{\text{h}}_{\text{n}}}\, = \,\,\,{e^{2n}}h\)

બોલ અટક્યાં ફેલા તેના દ્વારા કપટુ અંતર :

\({\text{S}}\,\, = \,\,{\text{h}}\,{\text{ }} + \,\,{\text{2}}{{\text{h}}_{\text{1}}}\,\, + \,\,2{h_2}\, + \,\,\,...............\,\, + \,\,\infty \)

\( = \,\,h\,\, + \,\,2{e^2}h\,\, + \,\,2{e^4}h\,\, + \,\,2{e^6}h\,\,\, + \,\,\,.............\)

\( = \,\,h\,\, + \,\,2{e^2}h\,(1\,\, + \,\,{e^2}\, + \,\,{e^4}\, + \,\,{e^6}\, + \,\,...........)\)

\(S\,\, = \,\,h\,\, + \,\,2{e^2}h\,\,\left( {\frac{1}{{1\,\, - \,\,{e^2}}}} \right)\,\,\, = \,\,\,h\,\,\left[ {1\,\, + \,\,\,\frac{{2{e^2}}}{{1\,\, - \,\,{e^2}}}} \right]\,,\,\,\,S\,\, = \,\,h\,\left( {\frac{{1\,\, + \,\,{e^2}}}{{1\,\, - \,\,{e^2}}}} \right)\)