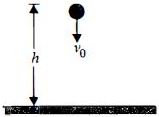
The situation is shown in the figure.
Let \(v\) be the velocity of the ball with which it collides with ground. Then according to the law of conservation of energy,
The situation is shown in the figure.
Let \(v\) be the velocity of the ball with which it collides with ground. Then according to the law of conservation of energy,
\(\begin{array}{l}
Gain\,in\,kinetic\,energy\, = loss\,in\,potential\\
energy\,i.e.\,\frac{1}{2}m{v^2} - \frac{1}{2}mv_0^2 = mgh\\
\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {where\,m\,is\,the\,mass\,of\,the\,ball} \right)\\
or\,\,\,{v^2} - v_0^2 = 2gh\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( i \right)\\
Now,\,when\,the\,ball\,collides\,with\,the\,\\
ground,\,50\% \,of\,its\,energy\,is\,lost\,and\\
it\,rebounds\,to\,the\,same\,height\,h.
\end{array}\)
\(\begin{array}{l}
\therefore \,\,\,\,\,\frac{{50}}{{100}}\left( {\frac{1}{2}m{v^2}} \right) = mgh\\
\frac{1}{4}{v^2} = gh\,\,or\,\,{v^2} = 4gh\\
Subsitiuding\,this\,value\,of\,{v^2}\,in\,eqn.\\
\left( i \right),\,we\,get\\
\,\,\,\,\,\,\,\,4\,gh\, - v_0^2 = 2gh\\
or\,\,\,\,\,\,v_0^2\, = 4gh - 2gh - 2gh\,\,or\,\,{v_0} = \sqrt {2gh}
\end{array}\)
\(\begin{array}{l}
Here,\,g\, = 10\,m{s^{ - 2}}\,and\,h = 20\,m\\
\therefore \,\,\,\,{v_0} = \sqrt {2\left( {10\,m{s^{ - 2}}} \right)\left( {20m} \right)} = 20m{s^{ - 1}}
\end{array}\)
Download our appand get started for free
Similar Questions
- 1અચળ ઝડપ $10\;ms^{-1}$ થી $x -$ દિશામાં $10 \;kg$ દળનો બ્લોક ગતિ કરતાં બ્લોક પર $F=0.1x \;\frac{J}{m}$ જેટલું અવરોધક બળ $ x= 20\;m$ થી $x=30\;m $ ની ગતિ દરમિયાન લાગે છે. તેની અંતિમ ગતિઊર્જા ($J$ માં) કેટલી હશે?View Solution
- 2View Solutionવિધાન: જો બે સ્થિતિસ્થાપક પદાર્થો વચ્ચે સંઘાત થાય તો સંઘાત દરમિયાન તેમની ગતિઉર્જા ઘટે છે.
કારણ: સંઘાત દરમિયાન આંતરણ્વીય જગ્યા ઘટે છે અને સ્થિતિઉર્જા વધે છે.
- 3$100 m $ લંબાઇ અને $1 m$ ઉંચાઇ ધરાવતા ઢાળ પર $30,000 kg$ નો ટ્રક $30 km/hr$ ની ઝડપથી ગતિ કરે,તો ટ્રકનો પાવર કેટલા .......... $kW$ થશે? $( g = 10m{s^{ - 1}}) $View Solution
- 4$m$ દળ એક બ્લોક ને $\frac{g}{3}$ અચળ પ્રવેગે શિરોલંબ રીતે ઉપર તરફ $h$ અંતર જેટલું ખેંચવા માટે એક દોરીના ઉપયોગ કરવામાં આવે છે. દોરીમાંના તણાવ વડે થયેલ કાર્ય છે...View Solution
- 5સ્થિર સ્થિતિમાં રહેલા $m$ દળના પદાર્થ પર બળ લાગતાં $t_1$ સમયમાં $v_1$ વેગ પ્રાપ્ત કરે છે.તો $t$ સમય પછી પાવર કેટલો થાય?View Solution
- 6$60$ ફૂટ ઉંચા મકાન પરથી $2 \;kg$ દળના એક બોલને અને $4 kg$ દળના બીજા બોલને એક સાથે ફેંકવામાં આવે છે. બંને બોલ પૃથ્વીની દિશામાં $30$ ફૂટ ઉંચાઈએથી પડ્યા પછી તેમની અનુક્રમે ગતિઊર્જાનો ગુણોત્તર કેટલો હશે ?View Solution
- 7$5 kg$ નો એક પદાર્થ સ્થિર સ્થિતિમાંથી ત્રણ ભાગમાં ફાટે છે ત્રણેય ભાગના દળનો ગુણોત્તર $1 : 1 : 3 $ છે. સમાન બળ ધરાવતા ભાગો એક બીજાને લંબ દિશામાં $21 m/s$ ના વેગથી ગતિ કરે છે તો સૌથી ભારે ભાગનો વેગ કેટલા.......$m/s$ ?View Solution
- 8$L$ લંબાઈના એક હલકા સળિયાને ઉપરના છેડાની શરૂઆતમાં મુકેલો છે. બે દળો (દરેકનું $m $ દળ) સળિયા સાથે જોડાયેલા છે. જેમાં એક સળિયાના મધ્યબિંદુએ અને બીજો દળ મુક્ત છેડે છે. નીચેના દળના છેડા આગળ કેટલો સમક્ષિતિજ વેગ લાગુ પાડવો જોઈએ કે જેથી સળિયો સમક્ષિતિજ રીતે રહે.View Solution
- 9શરૂઆતમાં ઉગમબિંદુ પર સ્થિર રહેલ એક $m$ દળની મોટરગાડીનું એન્જિન અચળ પાવર $P$ આપતા તે પ્રવેગી ગતિ કરે છે. તો તેનું સ્થાન સમયના વિધેય સ્વરૂપે કઈ રીતે દર્શાવી શકાય?View Solution
- 10એક કણને પૃથ્વીની સપાટીથી $S$ ઊંચાઈએથી છોડવામાં આવે છે. કોઈ ચોક્કસ ઊંચાઈએ તેની ગતિઊ તેની સ્થિતિઊર્જા કરતાં ત્રણ ગણી વધારે છે. આ ક્ષણે કણની પૃથ્વીની સપાટીથી ઊંચાઈ અને ઝડપ અનુક્રમે $.....$ છે.View Solution
