The given situation can be represented as shown in the following figure
Where, \(AO =\) Incident path of the ball
\(OB =\) Path followed by the ball after deflection
\(\angle AOB =\) Angle between the incident and deflected paths of the ball \(=45^{\circ}\)
\(\angle AOP =\angle BOP =22.5^{\circ}=\theta\)
Initial and final velocities of the ball \(=v\)
Horizontal component of the initial velocity \(=v \cos \theta\) along \(RO\)
Vertical component of the initial velocity \(=v \sin \theta\) along \(PO\)
Horizontal component of the final velocity \(=v \cos \theta\) along \(OS\)
Vertical component of the final velocity \(=v \sin \theta\) along \(OP\)
The horizontal components of velocities suffer no change. The vertical components of velocities are in the opposite directions.
\(\therefore\) Impulse imparted to the ball \(=\) Change in the linear momentum of the ball \(=m v \cos \theta-(-m v \cos \theta)\) \(=2 m v \cos \theta\)
Mass of the ball, \(m=0.15\, kg\)
Velocity of the ball, \(v=54 \,km / h =15 \,m / s\)
\(\therefore \text { Impulse }=2 \times 0.15 \times 15 \cos 22.5^{\circ}=4.16\, kg\, m / s\)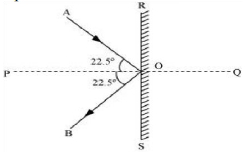
Download our appand get started for free
Similar Questions
- 1$\vec v$ જેટલા વેગથી ગતિ કરતાં એક કણ પર ત્રણ બળો લાગે છે.આ બળોના મૂલ્ય અને દિશાને આકૃતિમાં દર્શાવ્યા મુજબ ત્રિકોણની પાસપાસેની બાજુઓ વડે દર્શાવી શકાય,તો આ કણ કેટલા વેગથી ગતિ કરતો હશે?View Solution
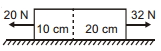
- 2આકૃતિમાં દર્શાવેલ $30 \,cm$ લાંબા નિયમિત સળિયાનો દળ $3.0 \,kg$ છે. આ સળિયાને $20 \,N$ અને $32 \,N$ નાં અચળ બળો દ્વારા ખેંચવામાં આવે છે. સળિયાના $10 \, cm$ ભાગ પર $20 \,cm$ ભાગ દ્વારા લગાડેલું બળ ...............$N$. (તમામ સપાટી લીસી છે)View Solution
- 3એક પદાર્થ સ્થિર સ્થિતિએ છે જે તૂટીને ત્રણ ટુકડાઓમાં રૂપાંતર પામે છે. સમાન દળના બે ટુકડાઓ $30\; m/s $ ની સમાન ઝડપ સાથે એકબીજાને લંબ ઉડ્ડયન કરે છે. ત્રીજા ટુકડાનું દળ બીજા ટુકડાઓના દળ કરતા ત્રણ ગણુ છે. વિસ્ફોટ થયા પછી તરત જ તે ટુકડાઓની દિશા અને વેગનું મૂલ્ય શું હશે ?View Solution
- 4એક લિફ્ટની છત પર સ્પ્રિંગ બેલેન્સ ગોઠવેલ છે.જયારે લિફ્ટ સ્થિર હોય ત્યારે એક માણસ પોતાની બેગ આ બેલેન્સ પર લટકાવે છે ત્યારે તેનું વજન $49\, N$ નોંધાય છે,તો લિફ્ટ જયારે $5 ms^{-2}$ ના પ્રવેગથી અધોદિશામાં ગતિ કરે ત્યારે આ બેગનું વજન ......... $N$ નોંધાશે.View Solution
- 5$1000\;kg$ ના રોકેટમાં બળતણના વપરાશનો દર $ 40 kg/s$ છે. રોકેટમાંથી બહાર આવતાં વાયુનો વેગ $5 \times {10^4}m/s$ છે. તો રોકેટ પર કેટલું બળ લાગતું હશે?View Solution
- 6$3 m$ દળનો સ્થિર બોમ્બ ફૂટતા ત્રણ સમાન ટુકડા થાય છે.બે ટુકડાના વેગ $ v\hat j $ અને $ v\hat i $ .હોય,તો ત્રીજા ટુકડાનો વેગ કેટલો થાય?View Solution
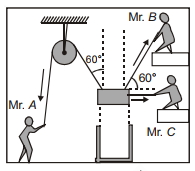
- 7શ્રીમાન $A, B$ અને $C$ રેલવે યાર્ડની યાંત્રિક વર્કશોપમાં ભારે પિસ્ટમને સિલિન્ડરમાં મુકવાનો પ્રયાસ કરી રહ્યા છે. જો તેઓ દોરડા પર અનુક્રમે $F_1, F_2$ અને $F_3$ બળો લગાડતા હોય, તો તે ક્ષણ પર બળોનાં ક્યા સમૂહ વડે, તેઓ પોતાનું કામ સારી રીતે પૂરું પાડી શકશે?View Solution
- 8એક ફુગ્ગાનું હવામાં દળ $10 \,g$ છે. ફુગ્ગામાંથી $4.5 \,cm / s$ ની નિયમીત ઝડપથી હવા નિકળે છે. જો ફૂગ્ગો $5 \,s$ માં સંપૂર્ણ ખાલી થઈ જાય તો ફુગ્ગા ઉ૫૨ લાગતું સરેરાશ બળ ........... $dyne$ થશે.View Solution
- 9$M$ દળની તકતીને હવામાં સ્થિર રાખવા માટે $6 m/sec$ ના વેગથી $1 \,sec$ માં $40$ પથ્થર અથડાવવામાં આવે છે.જો પથ્થરનું દળ $0.05\, kg$ હોય,તો તકતીનું દળ ........... $kg$ હશે. $(g = 10\,m{s^{ - 2}})$View Solution
- 10$M$ દળના બ્લોકને $M / 2$ દળના દોરડા વડ સક્ષિતિજ ઘર્ષણરહિત સપાટી પર ખેંચવામાં આવે છે. જો દોરડાના એક છેડા પર $2\,mg$ બળ લાગે તો, બ્લોક પર લાગતુ બળ $..........$View Solution
