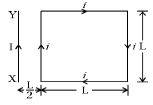
Force on arm \(A B\) due to current in conductor \(X Y\) is
\({F_1} = \frac{{{\mu _0}}}{{4\pi }}\frac{{2IiL}}{{(L/2)}} = \frac{{{\mu _0}Ii}}{\pi }\)
acting towards \(X Y\) in the plane of loop. Force on arm \(C D\) due to current in conductor \(X Y\) is
\({F_2} = \frac{{{\mu _0}}}{{4\pi }}\frac{{2IiL}}{{3(L/2)}} = \frac{{{\mu _0}Ii}}{{3\pi }}\)
acting away from \(X Y\) in the plane of loop.
\(\therefore\) Net force on the loop \(=F_{1}-F_{2}\)
\(=\frac{\mu_{0} I i}{\pi}\left[1-\frac{1}{3}\right]=\frac{2}{3} \frac{\mu_{0} I i}{\pi}\)
Download our appand get started for free
Similar Questions
- 1$I, II, III,IV.$ લૂપની સ્થિતિઊર્જા ઘટતા ક્રમમાં નીચે પૈકી કઈ છે?View Solution
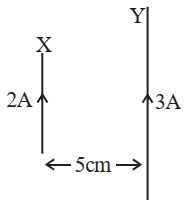
- 2$50\,cm$ લંબાઈના એક તાર $X$ને અને $2\; A$ પ્રવાહ ધરાવતા $5\,m$ લાંબા તાર $Y$ ને સમાંતર મૂકવામાં આવેલ છે. તાર માં $3\; A$ પ્રવાહ વહે છે. બે તારો વચ્ચેનું અંતર $5\,cm$ અને તેમાં સમાન દિશામાં પ્રવાહ વહે છે. $Y$ તાર ઉપર લાગતું બળ $..........$ હશે.View Solution
- 3બે સમાંતર રહેલા પ્રવાહધારિત તાર વચ્ચેનું અંતર $b$ છે.તો એક તાર દ્વારા બીજા તારના એકમ લંબાઇ દીઠ કેટલું બળ લાગશે?View Solution
- 4નીચે બે વિધાનો આપેલા છે.View Solution
વિધન $I:$ ચલિત ગૂંચળાવાળા ગેલ્વેનોમીટરમાં ગૂંચળાના આંટાની સંખ્યા બમણી કરતાં તેની પ્રવાહ સંવેદિતા બમણી થાય.
વિધન $II$ : ફક્ત ગૂંચળાના આંટાની સંખ્યા વધારીને ચલિત ગૂંયળાવાળા ગેલ્વેનીમીટર પ્રવાહ સંવેદિતા વધારતા તેની વોલ્ટેજ સંવેદિતા પણ તેટલા જ ગુણોત્તર પ્રમાણે વધશે.
ઉપર્યુક્ત કથનોના સંદર્ભમાં, નીચે આપેલા વિકલ્પોમાંથી સાયો ઉત્તર પસંદ કરો.
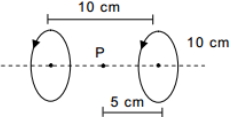
- 5$10$ સેમી ત્રિજ્યા અને $\frac{7}{2}\, A$ પ્રવાહ ધારીત બે લૂપને સમઅક્ષીય મૂકેલી છે, તેમના કેન્દ્ર વચ્ચેનું અંતર $10$ સેમી છે,તો $P$ બિંદુ પાસે ચુંબકીય ક્ષેત્ર શોધો.View Solution
- 6$R$ ત્રિજયાની રીંગના કેન્દ્ર આગળ અને કેન્દ્રથી $3R$ અંતરે અક્ષ પરના બિંદુએ ચુંબકીયક્ષેત્રનો ગુણોતર કેટલો થાય?View Solution
- 7એક સમાન ગતિઊર્જા સાથે ગતિ કરતો એક ડ્યુટેરોન અને પ્રોટોન નિયમિત (સમાન) યુંબકીય ક્ષેત્રમાં લંબરૂપે દાખલ થાય છે. જો $r_{d}$ અને $r_{p}$ અનુક્રમે તેમના વર્તુળાકાર પથની ત્રિજ્યાઓ હોય તો $\frac{r_{d}}{r_{p}}$ ગુણોત્તર $\sqrt{x}: 1$ છે. $x$ નું મૂલ્ય ......... થશે.View Solution
- 8'$a$' ત્રિજ્યાના એક સુરેખ વાહક તાર સ્થિર પ્રવાહ $I$ નું વહન કરે છે. આ પ્રવાહ્ સમગ્ર આડછેદ પર વિતરીત થયેલ છે. તારની અક્ષથી $\frac{a}{2}$ અને $2 \mathrm{a}$ અંતર આગળના ચુંબકીય ક્ષેત્રનો ગુણોતર . . . . .છે.View Solution
- 9$50\,\Omega$ અવરોધ અને $100\,μA$ પૂર્ણસ્કેલ આવર્તન ધરાવતા ગેલ્વેનોમીટરનું રૂપાંતર $10\,A$ માપી શકે તેવા એમિટરમાં કરવા માટે જરૂરી શંટ અવરોધ .......View Solution
- 10પ્રોટોનને પ્રવેગિત કરવા માટે સાઈક્લોટ્રોનનો ઉપયોગ કરવામાં આવે છે. જે કાર્યરત ચુંબકીય ક્ષેત્ર $1.0\,T$ હોય અને સાઈક્રલોટ્રોનના '$dees$' ની ત્રિજ્યા $60\,cm$ હોય તો પ્રવેગિત પ્રોટોનની ગતિ ઊર્જા $.....$ ( $MeV$ માં) હશે.View Solution
[$m _{p}=1.6 \times 10^{-27} kg , e =1.6 \times 10^{-19} C$ નો ઉપયોગ કરવો.]
