એક દડાને $t=0 $ સમયે સ્થિર સ્થિતિમાંથી ખૂબ ઊંચા પ્લેટફોર્મ પરથી છોડવામાં આવે છે. $6$ સેકન્ડ બાદ બીજા દડાને તે જ પ્લેટફોર્મ પરથી $v$ ઝડપથી નીચે ફેંકવામાં આવે છે. બંને દડા $t=18\;s$ ના સમયે એકબીજાને મળે છે. $v $ નું મૂલ્ય ($m/s$ માં) કેટલું હશે? ($g= 10\; ms^{-2}$ લો)
AIPMT 2010, Medium
a
Let the two balls meet a fter t s at distance x from the platform.
x from the platforam
For the first ball
\(u = 0,\,t = 18\,s,\,g = 10\,m/{s^2}\)
Using \(h = ut + \frac{1}{2}g{t^2}\)
\(\therefore \,\,\,\,x = \frac{1}{2} \times 10 \times {18^2}\)
For the second ball
\(u = v,\,t = 12\,s,\,g = 10\,m/{s^2}\)
Using \(h = ut + \frac{1}{2}g{t^2}\)
\(\therefore x = v \times 12 + \frac{1}{2} \times 10 \times {12^2}\)
From equations (\(i\)) and (\(ii\)), we get
Let the two balls meet a fter t s at distance x from the platform.
x from the platforam
For the first ball
\(u = 0,\,t = 18\,s,\,g = 10\,m/{s^2}\)
Using \(h = ut + \frac{1}{2}g{t^2}\)
\(\therefore \,\,\,\,x = \frac{1}{2} \times 10 \times {18^2}\)
For the second ball
\(u = v,\,t = 12\,s,\,g = 10\,m/{s^2}\)
Using \(h = ut + \frac{1}{2}g{t^2}\)
\(\therefore x = v \times 12 + \frac{1}{2} \times 10 \times {12^2}\)
From equations (\(i\)) and (\(ii\)), we get
\(\frac{1}{2} \times 10 \times {18^2} = 12v + \frac{1}{2} \times 10 \times {\left( {12} \right)^2}\)
or \(12v = \frac{1}{2} \times 10 \times \left[ {{{\left( {18} \right)}^2} - {{\left( {12} \right)}^2}} \right]\)
\( = \frac{1}{2} \times 10 \times \left[ {\left( {18 + 12} \right)\left( {18 - 12} \right)} \right]\)
\(12v = \frac{1}{2} \times 10 \times 30 \times 6\)
or \(v = \frac{{1 \times 10 \times 30 \times 6}}{{2 \times 12}} = 75\,m/s\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1સ્થિર સ્થિતિમાંથી કાર $a$ પ્રવેગથી $t=0$ થી $t=T$ સુધી ગતિ કરે છે.પછી પ્રતિપ્રવેગથી સ્થિર થઇ જાય છે તો તેની સરેરાશ ઝડપ કેટલી થાય?View Solution
- 2એક પદાર્થ $40 \,m / s$ ની ઝડપ સાથે ઉપરની તરફ પ્રક્ષિપ્ત કરેલ છે. ઉપર તરફની મુસાફરીના અંતિમ બીજા ભાગમાં પદાર્થ દ્વારા કપાયેલ અંતર ......... $m$ થાય? [$g =9.8\, m / s ^2$ અને હવાના અવરોધને અવગણો]View Solution
- 3એક ઢોળાવ વાળા સમતલ પર એક નાનકડો બ્લોક ઘર્ષણ રહિત ગતિ કરે છે. ધારો કે ${S_n}$ એ $t = n - 1$ to $t = n$ સમય માં કાપેલું અંતર છે તો $\frac{{{S_n}}}{{{S_{n + 1}}}}$ શું થાય?View Solution
- 4પ્રિતી મેટ્રો સ્ટેશન પર પહોંચીને જુએ છે, કે એસ્કેલેટર કાર્યરત નથી.તેથી તેને સ્થિર એસ્કેલેટર પર ચાલવા માટે $ t_1 $ સમય લાગે છે. બીજા દિવસે જ્યારે એસ્કેલેટર ચાલતું હોય, તો તે તેના પર ઊભા રહીને $t _{2}$ સમયમાં તે ઉપર પહોંચે છે. તે ગતિ કરતાં એસ્કેલેટર પર ચાલવા લાગે, તો તેને ઉપર પહોંચવા લાગતો સમય શું હશે?View Solution
- 5અચળ પ્રવેગથી ગતિ કરતી ટ્રેનનું એન્જિન સિગ્નલ પોસ્ટ (થાંભલા) ને $u$ વેગથી અને છેલ્લો ડબ્બો $v$ જેટલા વેગથી પસાર થાય છે. ટ્રેનનો મધ્યભાગ આ સિગ્નલ પોસ્ટને કેટલા વેગથી પસાર થશે?View Solution
- 6$80 \,m$ ની ઉંચાઈની મકાનની ટોચ પરથી બોલ નીચે ફેંકવામાં આવ્યો છે. આ જ ક્ષણ પર બીજો બોલ મકાનના તળિયેથી $50 \,m / s$ ની ઝડપ સાથે ઉપરની તરફ ગતિ કરે છે. ........ સેકેન્ડે પર બંને બોલ મળશે ?View Solution
- 7એક ઢોળાવ વાળા સમતલ પર એક નાનકડો બ્લોક ઘર્ષણ રહિત ગતિ કરે છે. ધારો કે ${S_n}$ એ $t = n - 1$ to $t = n$ સમય માં કાપેલું અંતર છે તો $\frac{{{S_n}}}{{{S_{n + 1}}}}$ શું થાય?View Solution
- 8$60 \,km/h$ ઝડપે ગતિ કરતા વાહનને બ્રેક લગાવ્યા બાદ તે $20\, m$ જેટલું અંતર કાપીને ઊભું રહે છે.આ વાહન બમણી ઝડપથી (એટલે કે $120 \,km/h$ થી ) ગતિ કરતું હોય, તો વાહનનું સ્ટોપિંગ ડિસ્ટન્સ ($m$ માં) કેટલું થાય?View Solution
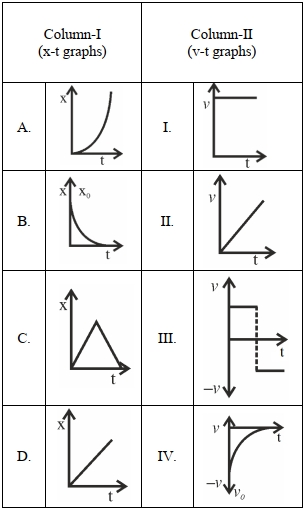
- 9સૂચિ$-I$ અને સૂચિ$-II$ ને સરખાવો.View Solution
નીચે આપેલા વિકલ્પોમાંથી સાચો જવાબ પસંદ કરો.
- 10$9.8\, m$ લંબાઇ ધરાવતા ઢાળ પરથી એક પદાર્થને પડતો મૂકવામાં આવે છે.તો પદાર્થ ઢાળના તળિયે કેટલા..........$sec$ સમય પછી પહોંચે?View Solution