એક ઢોળાવવાળા સમતલને એવી રીતે વાળવામાં આવે છે કે જેથી ઉર્ધ્વ આડછેદ $y=\frac{x^{2}}{4}$ થી આપી શકાય, જ્યાં , $y$ એ ઉર્ધ્વ દિશા અને $x$ સમક્ષિતિજ દિશા છે. જે આ વક્ર સમતલની ઉપરની સપાટી $\mu=0.5$ જેટલા ઘર્ષણાંક સાથે ખરબચડી હોય તો એક સ્થિર બ્લોક (ચોસલું) નીચે સરકે નહીં તે મહત્તમ ઊંચાઈ ...........$cm$ હશે
JEE MAIN 2021, Diffcult
b
At maximum ht. block will experience maximum friction force. Therefore if at this height slope of the tangent is \(\tan \theta,\) then \(\theta=\) Angle of repose.
At maximum ht. block will experience maximum friction force. Therefore if at this height slope of the tangent is \(\tan \theta,\) then \(\theta=\) Angle of repose.
\(\therefore \tan \theta=\frac{d y}{d x}=\frac{2 x}{4}=\frac{x}{2}=0.5\)
\(\Rightarrow x=1\) and therefore \(y=\frac{x^{2}}{4}=0.25 m\)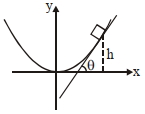
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1કોલમ $-I$ ને કોલમ $-II$ સાથે યોગ્ય રીતે જોડો.View Solution
કોલમ $-I$ કોલમ $-II$ $(1)$ સ્થિત ઘર્ષણ $(a)$ સીમાંત ઘર્ષણ $(2)$ રોલિંગ ઘર્ષણ $(b)$ બૉલબેરિંગ $(c)$ રસ્તા પર ગતિ કરતો પદાર્થ - 2View Solutionસમક્ષિતિજ રસ્તા પર થતી કારની પ્રવેગી ગતિ શાને આભારી છે
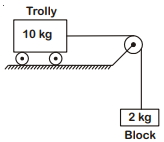
- 3આકૃતિમાં દર્શાવેલ ટ્રૉલી અને બ્લોકનો પ્રવેગ ($m/s^{2}$ માં ) શોધો જ્યાં ટ્રૉલી અને સપાટી વચ્ચેનો ઘર્ષણાક $0.05$ છે $\left( g =10\; m / s ^{2},\right.$ દોરીનું દળ અવગણ્ય છે અને બીજું કોઈ ઘર્ષણબળ લાગતું નથી).View Solution
- 4કોલમ $-I$ ને કોલમ $-II$ સાથે યોગ્ય રીતે જોડો.View Solution
કોલમ $-I$ કોલમ $-II$ $(1)$ સ્થિત ઘર્ષણ $(a)$ સીમાંત ઘર્ષણ $(2)$ રોલિંગ ઘર્ષણ $(b)$ બૉલબેરિંગ $(c)$ રસ્તા પર ગતિ કરતો પદાર્થ - 5બરફના બ્લોકને $\theta=45^°$ ઢાળવાળા રફ ઢાળ પરથી નીચે આવતા લાગતો સમય એ સમાન ઘર્ષણરહિત ઢાળ પરથી નીચે આવતા લાગતા સમય કરતાં બમણો હોય તો બ્લોક અને ઢાળ વચ્ચેનો ઘર્ષણાંક કેટલો હશે?View Solution
- 6$5 \,kg$ નો બ્લોક અને સપાટી વચ્ચેનો ઘર્ષણાંક $0.2$ છે. તેના પર $F= 40 \,N$ બળ લગાવતા બ્લોક ........ $m/s^2$ પ્રવેગ પ્રાપ્ત કરશે.View Solution

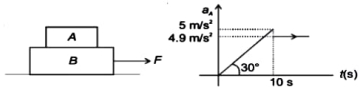
- 7આકૃતિમાં દર્શાવ્યા મુજબ બ્લોક $A$ નો પ્રવેગ એ સમયની સાપેક્ષે બદલાય છે, તો બ્લોક $A$ અને $B$ નો ગતિક ઘર્ષણાંકનું મુલ્ય ..... છે.View Solution
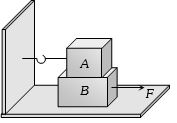
- 8$4\, kg$ દળ ધરાવતો બ્લોક $A$ ને બીજા $5\, kg$ દળ ધરાવતા બ્લોક $B$ પર મુકેલ છે અને બ્લોક $B$ એ લીસ્સા સમક્ષિતિજ ટેબલ પર પડ્યો છે. જો બંને બ્લોક ને એકસાથે ખસેડવા માટે $A$ પર લગાવવું પડતું ન્યુનત્તમ બળ $12\, N$ છે તો બંને બ્લોક ને સાથે ખસેડવા માટે $B$ પર લગાવવું પડતું મહત્તમ બળ ........ $N$ થાય.View Solution
- 9$A$ અને $B$ નું દળ $100 \,kg$ અને $200\,kg$ છે.$A$ અને $B$ વચ્ચેનો ઘર્ષણાંક $0.2$ અને $B$ અને જમીન વચ્ચેનો ઘર્ષણાંક $0.3$ હોય,તો $B$ ને ગતિ કરાવવા ....... $N$ બળ $F$ લગાવવું પડશે.View Solution
- 10વિધાન $I :$ એક સાઈકલ સવાર ઢોળાવ વગરના રસ્તા ઉપર $7\, kmh ^{-1}$ના ઝડપથી ગતિ કરે છે અને $2 \,m$ ની ત્રિજ્યા ધરાવતાં પથ પર પોતાની ઝડપ ઘટાડવા સિવાય એક sharp વળાંક લે છે. સ્થિત ઘર્ષણાંક $0.2$ છે. સાઈકલ સવાર સરક્તો નથી અને વળાંક પસાર કરે છે. $\left( g =9.8\, m / s ^{2}\right)$View Solution
વિધાન $II :$ જો રસ્તો $45^{\circ}$ ના કોણે ઢળેલા હોય તો સાઈકલ સવાર $2\, m$ ત્રિજ્યા ધરાવતો વળાંક સરક્યા સિવાય $18.5\, kmh ^{-1}$ની ઝડપ સાથે પસાર કરી શકે છે.
ઉપરોક્ત વિધાનોનાં સંદર્ભમાં, નીચે આપેલ વિકલ્પો પૈકી સાચો જવાબ પસંદ કરો :
