$\rho (r)\, = \,{\rho _0}\left( {1 - \frac{r}{R}} \right)$, $r < R$ માટે
$\rho (r)\,=\,0$, $r\, \ge \,R$ માટે
જ્યાં $r$ એ વિજભાર વિતરણના કેન્દ્રથી અંતર અને $\rho _0$ અચળાંક છે. $(r < R)$ ના અંદરના બિંદુ પાસે વિદ્યુતક્ષેત્ર કેટલું મળે?
Let us consider a spherical shell of radius \(x\) and thickness \(dx.\)
Charge on this shell
\(\mathrm{dq}=\rho 4 \pi \mathrm{x}^{2} \mathrm{dx}=\rho_{0}\left(1-\frac{\mathrm{x}}{\mathrm{R}}\right) .4 \pi \mathrm{x}^{2} \mathrm{dx}\)
\(\therefore\) Total charge in the spherical region from centre to \(r(r < R)\)
\(q=\int d q=4 \pi \rho_{0} \int_{0}^{T}\left(1-\frac{x}{R}\right) x^{2} d x\)
\(=4 \pi \rho_{0}\left[\frac{x^{3}}{3}-\frac{x^{4}}{4 R}\right]_{0}^{t}\)
\(=4 \pi \rho_{0}\left[\frac{r^{3}}{3}-\frac{r^{4}}{4 R}\right]\)
\(=4 \pi \rho_{0} r^{3}\left[\frac{1}{3}-\frac{r}{4 R}\right]\)
\(\therefore\) Electric field atr, \(\mathrm{E}=\frac{1}{4 \pi \varepsilon_{0}} \cdot \frac{\mathrm{q}}{\mathrm{r}^{2}}\)
\( = \frac{1}{{4\pi {\varepsilon _0}}} \cdot \frac{{4\pi {\rho _0}{r^3}}}{{{r^2}}} \cdot \left[ {\frac{1}{3} - \frac{r}{{4R}}} \right]\)
\(=\frac{\rho_{0}}{\varepsilon_{0}}\left[\frac{\tau}{3}-\frac{\tau^{2}}{4 R}\right]\)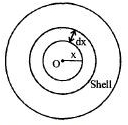
Download our appand get started for free
Similar Questions
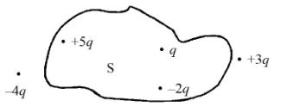
- 1પાંચ વિદ્યુતભારો $+q,+5 q,-2 q,+3 q$ અને $-4 q$ ને આક્રૂત્તિમાં દર્શાવ્યા અનુસાર ગોઠવવામાં આવ્યા છે.View Solution
સપાટી $s$ માંથી પસાર થતું આ વિદ્યુતભારોની ગોઠવણીને કારણે સંકળાયેલ ફ્લક્સ...........છે.
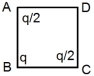
- 2$'a'$ બાજુ ધરાવતા ચોરસના ખૂણા (શિરોબિંદુ) $A, B$ અને $C$ ઉપર ત્રણ વિદ્યુતભારો $q/2, q$ અને $q/2$ મૂકેલા છે. (આકૃતિ જુઓ) બાકી રહેલા શિરોબિંદુ $D$ ઉપર વિદ્યુતક્ષેત્ર તીવ્રતાનું મૂલ્ય ........ હશે.View Solution
- 3$10\, mg$ દળ ધરાવતાં બે નાના ગોળાઓને $0.5\, m$ લંબાઈની દોરી દ્વારા એક બિંદુ પરથી લટકાવવામાં આવ્યા છે. બંને પર એક સરખો વિજભાર છે અને એકબીજાને $0.20\, m$ અંતર સુધી અપાકર્ષિત કરે છે. દરેક ગોળા પરનો વિજભાર $\frac{ a }{21} \times 10^{-8} \, C$ છે તો $a$ નું મૂલ્ય ........ હશે. [$g=10 \,ms ^{-2}$ આપેલ છે. ]View Solution
- 4દરેક $m$ જેટલું દળ અને $q$ જેટલો વિદ્યુતભાર ધરાવતા બે એકસમાન ટેનિસ બોલને $l$ લંબાઈની દોરી વડે જડિત બિંદુથી લટકવવામાં આવેલ છે. જ્યારે શિરોલંબ સાથે દરેક દોરી નાનો કોણ $\theta$ રચતી હોય તો ત્યારે સંતુલન સ્થિતિમાં અંતર .......... હશે?View Solution
- 5વિદ્યુતભાર $Q$ અને $-3Q$ અમુક અંતરે મૂકેલા છે,$Q$ પર વિદ્યુતક્ષેત્ર $E$ હોય,તો $-3Q$ પર વિદ્યુતક્ષેત્ર કેટલું થાય?View Solution
- 6$R$ ત્રિજયાના ગોળીય કવચમાં કેન્દ્રથી અંતર નો વિદ્યુતક્ષેત્ર $E$ વિરુધ્ધનો આલેખ કેવો થાય?View Solution
- 7ધારો કે એક નક્કર ગોળાની ત્રિજ્યા $R$ અને તેના પરનો વિદ્યુતભાર $Q$ છે. આ ગોળાનું વિદ્યુત ઘનતા વિતરણ $\rho( r )=\frac{ Q }{\pi R ^{4}} \cdot r$ સૂત્ર વડે અપાય છે. આ ગોળાની અંદર ગોળાના કેન્દ્રથી $r _{1}$ અંતરે આવેલા બિંદુ $P$ આગળ વિદ્યુતક્ષેત્રનું મૂલ્ય કેટલું થાય?View Solution
- 8$1\, g$ જેટલા સમાન દળના બે સમાન ગોળાઓ પરનો સમાન વિદ્યુતભાર $10^{-9}\, C$ છે. જેમને સમાન લંબાઈની દોરીઓ વડે મુક્ત કરવામાં આવે છે. જો ગોળાનો કેન્દ્રો વચ્ચેનું અંતર $0.3\, cm$ હોય તો દોરીના પ્રક્ષેપણ કોણ શિરોલંબ ઘટક સાથે ...... હશે.View Solution
- 9જો ડાઇપોલની અક્ષ પર $x$ જેટલા અંતરે વિદ્યુતક્ષેત્રની તિવ્રતા તેની વિષૃવરેખા પર $y$ જેટલા અંતરે વિદ્યુતક્ષેત્રની તિવ્રતા સમાન હોય તો $x:y$ ....View Solution
- 10$10\ cm$ ત્રિજયા ધરાવતા ગોળાથી $20\ cm$ અંતરે વિદ્યુતક્ષેત્ર $100\ V/m$ છે.તો કેન્દ્રથી $3\ cm$ અંતરે વિદ્યુતક્ષેત્ર કેટલા .....$V/m$ થાય?View Solution
