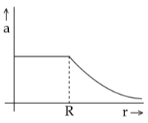
એક ગોળાકાર પદાર્થની ઘનતા $\rho \left( r \right) = \frac{k}{r}$ જ્યાં $r \leq R\,\,$ અને $\rho \left( r \right) = 0\,$ $r > R$ માટે ,મુજબ આપવામાં આવે છે જ્યાં $r$ એ કેન્દ્રથી અંતર છે. નીચેનામાંથી કયો પ્રવેગ $a$ નો અંતર $r$ વિરુદ્ધનો ગ્રાફ સાચો છે ?
JEE MAIN 2017, Diffcult
b
Give that, mass desity \(\left( {\frac{{mass}}{{volume}}} \right)\) of a
Give that, mass desity \(\left( {\frac{{mass}}{{volume}}} \right)\) of a
spherical body \(\rho \left( r \right) = \frac{k}{r}\)
\(\frac{M}{V} = \frac{k}{r}\,for\,inside\,r \le R\)
\(M = \frac{{kv}}{r}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,...\left( i \right)\)
Inside the surface of sphere Intensity
\(I = \frac{{GMr}}{{{R^3}}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,I = \frac{F}{m}\)
\({g_{inside}} = \frac{{GMr}}{{{R^3}}}\,\,\,\,\,\,\,\,\,\,\,or\,\,\,\,\,\,\,\,\,\,I = \frac{{mg}}{m} = g\)
\( = \frac{G}{{{R^3}}}\frac{{kv}}{r}.r = constant\,\,\,\,\,From\,eq.\,\left( i \right),\)
\(similarly,\,{g_{out}} = \frac{{GM}}{{{r^2}}}\)
Hence, option \((b)\) is correct graph.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1ચંદ્રને પૃથ્વી ફરતે $1$ પરિભ્રમણ પૂર્ણ કરતાં $29$ દિવસ લાગે છે .જો ચંદ્રનું દળ બમણું કરવામાં આવે પણ બીજા બધા પરિમાણ પહેલા જેટલા રાખવામા આવે તો 1 પરિભ્રમણ પૂર્ણ કરતાં લાગતો સમય ....... $(day)$ થાય ?View Solution
- 2જો ચંદ્રનું દળ $7.34 \times {10^{22}}\,kg$ અને ત્રિજ્યા $1.74 \times {10^6}\,m$ હોય તો ચંદ્ર પર ગુરુત્વપ્રવેગનું મુલ્ય ....... $N/kg$ થાય.View Solution
- 3View Solutionએક કણ અનંત અંતરે થી પૃથ્વી પર આવે તો તો તેનો વેગ કેટલો હશે?
- 4$A$ અને $B$ સેટેલાઈટ સમાન ગ્રહની ફરતે એક જ સમતલમાં રહેલી વર્તુળાકાર કક્ષામાં ભ્રમણ કરે છે. તેમના આવર્તકાળ અનુક્રમે $1\, h$ અને $8\, h,$ છે. $A$ ની કક્ષીય ત્રિજ્યા is $10^{4} \;km$ હોય તો $B$ ની $A$ ની સાપેક્ષે ઝડપ ($k m / h$ માં) કેટલી થશે?View Solution
- 5View Solutionનીચેનામાથી ક્યૂ વિધાન સાચું છે : ભ્રમણ કરતાં ઉપગ્રહ માં રહેલા અવકાશયાત્રી નું ઓછું વજન એ પરિસ્થિતી
- 6બિંદુવત દળને પૃથ્વીની સપાટીથી $h$ ઊંંચાઈએ અને પૃથ્વીની સપાટીથી $\alpha h \left( h \ll < R _{ e }\right)$ જેટલી ઊંંડાઈએ ગુરુત્વાકર્ષણને કારણે ઉત્પન્ન પ્રવેગ સમાન અનુભવાય છે. $\alpha$ નું મૂલ્ય થશે.કારણે ઉત્પન્ન પ્રવેગ સમાન અનુભવાય છે. $\alpha$ નું મૂલ્ય થશે.$\text { ( } R _{ e }=6400\,km)$View Solution
- 7જો $R$ પૃથ્વીની ત્રિજ્યા અને પૃથ્વીની સપાટી પરનો ગુરુતવ્પ્રવેગ $g=\pi^2 \mathrm{~m} / \mathrm{s}^2$ છે તો પૃથ્વીની સપાટીથી $h=2 R$ ઉાંચાઈએ સેકંડ દોલકની લંબાઈ__________હશે.View Solution
- 8View Solutionએક ઉપગ્રહ પૃથ્વીની સપાટીની નજીક લંબગોળ કક્ષા માં ભ્રમણ કરે તો તેનો વેગ ......
- 9પૃથ્વીની સપાટીથી $4{R_e}$ ઊંચાઇ પર રહેલા $m$ દળના પદાર્થની નિષ્ક્રમણ ઊર્જા કેટલી થાય? ($R$= પૃથ્વીની ત્રિજયા)View Solution
- 10પૃથ્વીની ત્રિજયા લગભગ $6400\; km$ અને મંગળની ત્રિજયા $3200\; km$ છે. પૃથ્વીનું દળ, મંગળના દળ કરતાં લગભગ $10$ ગણું છે. પૃથ્વીની સપાટી પર કોઇ પદાર્થનું વજન $200 \;N$ છે. મંગળની સપાટી પર તેનું વજન ($N$ માં) કેટલું હશે?View Solution