એક હલકી મિટર સ્કેલ પર $1\,cm, 2\,cm,.........100 \,cm $ પર અનુક્રમે $1 \,g, 2\,g............ 100\, g$ વજન મૂકેલા હોય તો તંત્રને સમતોલન માં રાખવા માટે મિટર સ્કેલ ને ..... $cm$ આધાર રાખવો પડે.
Diffcult
c
\(\cdot\) Weights are \(1 \mathrm{g}, 2 \mathrm{g}, 3 \mathrm{g}, \ldots \ldots .100 \mathrm{g}\)
\(\cdot\) Weights are \(1 \mathrm{g}, 2 \mathrm{g}, 3 \mathrm{g}, \ldots \ldots .100 \mathrm{g}\)
\(\cdot\) Weights are suspended at a distance \(=1 \mathrm{cm}, 2 \mathrm{cm}, 3 \mathrm{cm}, \ldots \ldots .100 \mathrm{cm}\)
respectively to the masses.
For the system to be in equilibrium the point must lie in the center of mass.
So center of mass of the system can be calculated as
\(\mathrm{COM}=\frac {\left(1^{2}+2^{2}+3^{2} \ldots 100^{2}\right)} {(1+2+3 \ldots+100)}\)
\(COM = \left[ {\frac{{\frac{{\left( {100} \right)\left( {101} \right)\left( {201} \right)}}{6}}}{{\frac{{\left( {100} \right)\left( {101} \right)}}{2}}}} \right]\)
\(\mathrm{COM}=\frac {201}{3}=67 \mathrm{cm}\)
Hence at \(67 \mathrm{cm}\) from the origin or \(66 \mathrm{cm}\) from the first particle, at that point system will be supported to get equilibrium.
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક $500\; g$ દળનો ગોળો સમક્ષિતિજ સમતલમાં સરક્યાં વગર ગબડે છે.તેનું કેન્દ્ર $5.00\; \mathrm{cm} / \mathrm{s}$ ની ઝડપથી ગતિ કરતું હોય તો તેની ગતિઉર્જા કેટલી હશે?View Solution
- 2$l$ લંબાઇના અને $R$ ત્રિજયાવાળા એક યુનિફોર્મ નળાકારની તેના લંબ દ્વિભાજક સાપેક્ષ જશત્વની ચાકમાત્રા $I$ છે.ગુણોત્તર $l/R$ ના કયા મૂલ્ય માટે જડત્વની ચાકમાત્રા ન્યુનતમ થશે?View Solution
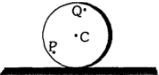
- 3તકતી સમક્ષિતિજ સપાટી પર (સરક્યા વિના) ગબડે છેે. $ C$ એ કેન્દ્ર અને $ Q$ અને $ P$ એ $ C $ થી સમાન અંતરે રહેલા બિંદુઓ છે. ધારો કે $v_P$, $ v_Q$, અને $ v_C$ એ અનુક્રમે બિંદુ $ P$, $Q$ અને $C $ ના વેગનું મૂલ્ય છે ત્યારે...View Solution
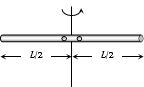
- 4View Solutionપદાર્થ સમક્ષિતિજ સપાટી પર સરક્યા સિવાય રોલિંગ કરે છે. તેની ચાકગતિ ઊર્જાએ સ્થાનાંતરિત ગતિ ઊર્જા જેટલી છે. તો પદાર્થ ....... છે.
- 5બે કણો ના તંત્ર વિશે વિચાર કરો. તેમાં થી એક કણ સ્થિર છે અને બીજો કણ $\vec{f}$ પ્રવેગ ધરાવે છે તો દ્રવ્યમાન કેન્દ્ર નો પ્રવેગ કેટલો થાય?View Solution
- 6એક ચક્રની જડત્વની ચાકમાત્રા $4\ kg - {m^2}$ અને ગતિઉર્જા $200\ J$ છે.તેના પર $5\ N-m$ નું ટોર્ક લગાવાથી તે સ્થિર થાય,ત્યાં સુધીમાં કરેલા પરિભ્રમણ .......... $rev$View Solution
- 7આપેલ અક્ષ પર પદાર્થની જડત્વની ચાકમાત્રા $1.2 \;kg m^{2}$ છે. પ્રારંભમાં પદાર્થ સ્થિર છે. $1500$ જૂલની ગતિઊર્જા ઉત્પન્ન કરવા માટે આપેલ અક્ષ પર $ 25\ rad/s^2 $ નો કોણીય પ્રવેગ કેટલા સમય ($sec$ માં) સુધી આપવો જોઈએ?View Solution
- 8આકૃતિમાં બતાવ્યા પ્રમાણે ઘનગોલક સપાટી પર રેખીય વેગ $v\,ms^{-1}$ થી ગબડે છે. જો તેને ઢાળ પર સરક્યાં વિના ચડાવવું હોય તો તેના માટે ન્યુનત્તમ વેગ કેટલો હોવો જોઈએ?View Solution

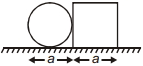
- 9નીચે દર્શાવ્યા પ્રમાણે ' $a$ ' વ્યાસ ની એક વર્તુળાકાર પ્લેટને $a$ બાજુ ની એક ચોરસ પ્લેટ સાથે સંપર્કમાં મુકવામાં આવે છે. બધી જ જગ્યાએ પદાર્થ ની ઘનતા અને જાડાઈ બધેજ સમાન છે. સંયુક્ત તંત્રનું દ્રવ્યમાન કેન્દ્ર શું થાય?View Solution
- 10View Solutionફ્લાય વ્હીલને એક એન્જિન સાથે વાપરવામાં આવે છે કારણ કે તે,
