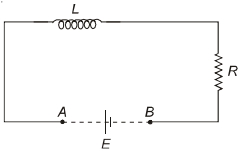
એક ઇન્ડકટર $(L=100\; mH)$ અવરોધ $(R =100\;\Omega)$ અને બેટરી $(E=100\; V)$ ને શરૂઆતમાં આકૃતિમાં દર્શાવ્યા પ્રમાણે શ્રેણીમાં જોડેલાં છે. ઘણા લાંબા સમય પછી $A$ અને $B$ શૉટસર્કિટ થતાં બેટરી દૂર થઈ જાય છે, તો શૉટસર્કિટ પછી પરિપથમાંથી $1\;ms$ પછી પસાર થતો પ્રવાહ $I$ ($A$ માં) કેટલો હશે?

AIEEE 2006, Diffcult
a
Initially, when steady state is achieved,
Initially, when steady state is achieved,
\(i=\frac{E}{R}\)
Let \(E\) is short circuited at \(t=0 .\) Then
At \(t=0, i_{0}=\frac{E}{R}\)
Let during decay of current at any time the current
flowing is \(-L \frac{d i}{d t}-i R=0\)
\(\Rightarrow \frac{d i}{i}=-\frac{R}{L} d t \Rightarrow \int_{i_{0}}^{i} \frac{d i}{i}=\int_{0}^{t}-\frac{R}{L} d t\)
\(\Rightarrow \log _{e} \frac{i}{i_{0}}=-\frac{R}{L} t \Rightarrow i=i_{0} e^{-\frac{R}{L} t}\)
\(\Rightarrow i=\frac{E}{R} e^{-\frac{R}{L} t}=\frac{100}{100} e^{\frac{-100 \times 10^{-3}}{100 \times 10^{-3}}}=\frac{1}{e}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1આકૃતિમાં દર્શાવેલ વીજપરિપથમાં કવોલીટી અવયવ અને બેન્ડવીડથનો ગુણોત્તર $.............s$ છે.View Solution
- 2એસી પરિપથમાં, વિદ્યુતસ્થિતિમાનનો તફાવત અને વિદ્યુતપ્રવાહ અનુક્રમે $V=10 \sqrt{2} \sin \omega t(V$ માં) અને $I=2 \sqrt{2} \cos \omega t$ ($V$ માં) છે. પરિપથમાં વપરાતો પાવર $............W$ છે.View Solution
- 3એક $LC$ દોલકમાં, જો ઈન્ડકટર અને સંધારકનું મૂલ્ય અનુક્રમે બમણું અને આઠગણું કરવામાં આવે તો દોલકની આવૃત્તિ તેની મૂળ પ્રાકૃતિક આવૃત્તિ $\omega_0$ કરતા $x$ નું મુલ્ય $.........$ થશે.View Solution
- 4એસી પરિપથમાં, વિદ્યુતસ્થિતિમાનનો તફાવત અને વિદ્યુતપ્રવાહ અનુક્રમે $V=10 \sqrt{2} \sin \omega t(V$ માં) અને $I=2 \sqrt{2} \cos \omega t$ ($V$ માં) છે. પરિપથમાં વપરાતો પાવર $............W$ છે.View Solution
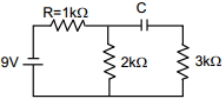
- 5જ્યારે કેપેસીટરમાં સંપૂર્ણ ચાર્જ થાય ત્યારે $9\, V $ ની બેટરીમાંથી નીકળતો પ્રવાહ શોધો. ($mA$ માં)View Solution
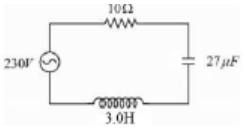
- 6જેમાં $L=10 \,mH , C =25 \mu F$ અને $R =100 \Omega$ હોય તેવા $LCR$ શ્રેણી પરિપથમાં એક જયાવર્તી વોલ્ટેજ $V(t)$ $=210 \sin 3000 t$ વોલ્ટ લગાડવામાં આવે છે. લગાવેલ વોલ્ટેજ અને પરિણામી પ્રવાહ વચ્ચે કળા તફાવત $(\Phi)$......... થશે.View Solution
- 7$4 \,A$ ના મૂલ્યનો $DC$ અને $4 \,A$ જેટલો મહત્તમ પ્રવાહ ધરાવતો $AC$ પ્રવાહ અનુક્રમે $3 \,\Omega$ અને $2 \,\Omega$ અવરોધોમાંથી વહે છે. બે અવરોધોમાં સમાન સમયમાં ઉત્પન્ન થતી ઉષ્માનો ગુુણોત્તર .......... થશે.View Solution
- 8$LCR$ પરિપથમાં વિદ્યુતસ્થિતિમાન કરતાં વિદ્યુતપ્રવાહ કઈ સ્થિતિમાં આગળ છે? ($\omega_0=$ અનુનાદ કોણીય આવૃત્તિ)View Solution
- 9$10\, mH$ ઇન્ડકટર અને $50\,\Omega$ અવરોધ ધરાવતી ટ્યુનિગ પરિપથને $1\,MHz$ આવૃતિ સિલેકશન માટે જરૂરી કેપેસિટન્સ ......$pF$ (લો : $\pi ^2 = 10)$View Solution
- 10એક $A.C.$ પરિપથમાં તાત્ક્ષણિક $emf$ અને પ્રવાહ નીચે મુજબ આપી શકાય છે.View Solution
$e=100$ $sin$ $20t$
$i=20sin$ $\left( {30t - \frac{\pi }{4}} \right)$ $A.C.$ ના એક સાઇકલ ( આવર્તન ) માટે પરિપથ દ્વારા ઉપયોગમાં લીધેલ પાવર (કાર્યત્વરા) અને $wattlesss$ પ્રવાહ અનુક્રમે _______ થશે.
