એક જૈવરાસાયણિક પ્રક્રમમાં એક પ્રક્રિયાની સક્રિયકરણ શક્તિ $532611\,J\,mol ^{-1}$ છે. જયારે તાપમાન $310\,K$ થી $300\,K$ માં ઓછું થાય ત્યારે જોવા મળતો વેગ અચળાંકમાં ફેફાર $k _{300}=x \times 10^{-3}\,k _{310}$ તો $x$ નું મૂલ્ય $.....$ છે.
[આપેલ: $\ln 10=2.3$$R =8.3\, J \, K ^{-1}\, mol ^{-1}$]
JEE MAIN 2022, Diffcult
a
\(\ln \left(\frac{ K _{2}}{ K _{1}}\right)=\frac{ E _{ a }}{ R }\left(\frac{1}{ T _{1}}-\frac{1}{ T _{2}}\right)\)
\(\ln \left(\frac{ K _{2}}{ K _{1}}\right)=\frac{ E _{ a }}{ R }\left(\frac{1}{ T _{1}}-\frac{1}{ T _{2}}\right)\)
\(\operatorname{\ell n}\left(\frac{ K _{2}}{ K _{1}}\right)=\frac{532611}{8.3}\times\left(\frac{10}{310 \times 300}\right)\)
where \(K _{2}\) is at \(310 \,K\) and \(K _{1}\) is at \(300 \,K\) \(\ln \left(\frac{ K _{2}}{ K _{1}}\right)=6.9\)
\(=3 \times \ell n 10\)
\(\ell n \frac{ K _{2}}{ K _{1}}=\ell n 10^{3}\)
\(K _{2}= K _{1} \times 10^{3}\)
\(K _{1}= K _{2} \times 10^{3}\)
So \(K=1\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionરાસાયણિક પ્રક્રિયા માટે કયો અપૂર્ણાંક કદાપિ હોઈ શકે નહિ?
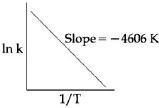
- 2એક પ્રક્રિયા માટે $ln k$ વિરૂદ્ધ $1/T$ નો આલેખ ધ્યાનમાં લો જ $400\, K$ એ આ પ્રક્રિયાનો વેગ અચળાંક $10^{-5}\,s^{-1},$ હોય, તો $500\, K$ એ વેગ અચળાંક કેટલો હશે?View Solution
- 3પ્રતિવર્તી પ્રક્રિયા $2N{O_2}\underset{{{K_2}}}{\overset{{{K_1}}}{\longleftrightarrow}}{N_2}{O_4}$ માટે $NO_2$ ના દૂર થવાનો દર....... થશેView Solution
- 4$A \rightarrow B$ પ્રક્રિયા પ્રથમ ક્રમ ગતિને અનુસરે છે. $0.8 $ મોલ $ A $ થી $0.6$ મોલ $B$ ના રૂપાંતર કરતા તેને $1$ કલાક જેટલો સમય થાય તો $0.9$ મોલ $ A$ થી $0.675$ મોલ $B$ ના રૂપાંતરને ......... કલાક લાગે.View Solution
- 5પ્રકિયા $A\rightarrow B$ નો વેગ અચળાંક$0.6 \times 10^{-3}\, mol\, L^{-1}\, s^{-1}.$ છે જો $A$ ની સાંદ્રતા $5\, M,$ છે ત્યારબાદ $20$ મિનિટ પછી $B$ ની સાંદ્રતા .......$M.$ હશેView Solution
- 6View Solutionજો પ્રથમ ક્રમની પ્રક્રિયામાં વાયુમય પ્રક્રિયક અને વાયુમય નિપજો આવેલ હોય તો તેના દર અચળાંક એકમ શું હશે?
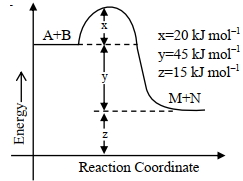
- 7નીચેના આંકડા મુજબ, પ્રક્રિયાના એન્થાલ્પી ફેરફારની તીવ્રતાView Solution
${A}+{B} \rightarrow {M}+{N}$ $......$ ${kJ} {mol}^{-1}$ બરાબર છે. (નજીકના પૂર્ણાંકમાં)
- 8$25 ^{\circ}\,C$ પર એક વાયુ $AB _3$ ના વિધટનનો અભ્યાસ એક વિદ્યાર્થીએ કર્યો તેને નીચે મુજબની માહિતી મેળવી.View Solution
$p ( mm Hg )$ $50$ $100$ $200$ $400$ સાપેક્ષ $t _{1 / 2}( s )$ $4$ $2$ $1$ $0.5$ પ્રક્રિયાનો ક્રમ શોધો.
- 9પ્રક્રિયાનું તાપમાન $300\, K$ થી $310\, K$ કરતા પ્રક્રિયાનો વેગ $2.5$ ગણો વધે છે. જો $300\, K$ તાપમાને પ્રક્યિાનો વેગઅચળાંક $K$ હોય, તો $310\, K$ તાપમાને વેગ અચળાંક કેટલો થશે ?View Solution
- 10પ્રથમ ક્રમ પ્રક્રિયાના કિસ્સામાં $99.9\% $ પૂર્ણ થી $50\%$ પૂર્ણ થવા માટેનો જરૂરી સમયનો ગુણોત્તર ......View Solution
