એક કણ અચળ પ્રવેગથી પ્રથમ $5 \,sec$ માં $10\, m$ અને પછીની $3 \,sec$ માં $10 \,m$ અંતર કાપે છે,તો ત્યાર પછીની $2 sec$ માં તે કેટલા.........$m$ અંતર કાપશે?
Diffcult
a
(a) Let initial \((t = 0)\) velocity of particle\( = u\)
(a) Let initial \((t = 0)\) velocity of particle\( = u\)
For first \(5\, sec\) motion \({s_5} = 10\;metre\)
\(s = ut + \frac{1}{2}a{t^2} \Rightarrow 10 = 5u + \frac{1}{2}a{(5)^2}\)
\(2u + 5a = 4\) …(i)
For first \(8 \,sec\) of motion \({s_8} = 20\;metre\)
\(20 = 8u + \frac{1}{2}a{(8)^2} \Rightarrow 2u + 8a = 5\) …(ii)
By solving \(u = \frac{7}{6}m/s\;{\rm{and }}a = \frac{1}{3}m/{s^2}\)
Now distance travelled by particle in Total \(10\) sec.
\({s_{10}} = u \times 10 + \frac{1}{2}a{(10)^2}\)
By substituting the value of \(u\) and \(a\) we will get \({s_{10}} = 28.3\;m\)
so the distance in last \(2\;\sec = {s_{10}} - {s_8}\)
\( = 28.3 - 20 = 8.3\,m\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1નીચેનામાંથી ક્યો સમય-સ્થાનાંતર આલેપ એ શૂન્ય સાપેક્ષ વેગ સાથે ગતિ કરતાં બે પદાર્થો $P$ અને $Q$ ને રજૂ કરે છે?View Solution
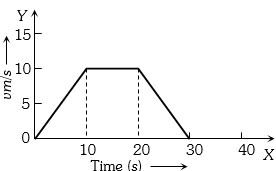
- 2આપેલ ગ્રાફ માટે પદાર્થે કાપેલ અંતર .......... $\mathrm{m}$ હશે.View Solution
- 3View Solutionપદાર્થનું સ્થાનાંતર તેના દ્વારા લાગતાં સમયના ધનના સમપ્રમાણ હોય તો પદાર્થના પ્રવેગનું મૂલ્ય .....
- 4એક કાર $200 \;m$ જેટલું અંતર કાપે છે.તે પ્રથમ અડધું અંતર $40 \;km / h$ ની ઝડપે કાપે છે. બાકીનું અડધું અંતર $v$ જેટલી ઝડપે કાપે છે.જો કારની સરેરાશ ઝડપ $48\; km / h$ હોય,તો $v$ નું મૂલ્ય ...... $km/h$ હશે.View Solution
- 5$3\,km/hr$ ની ઝડપથી ગતિ કરતી નદીમાં,હોડી $5\, km/hr$ ની ઝડપથી ગતિ કરે છે.નદીની પહોળાઇ $1\, km $ છે.હોડીને નદીને પાર કરીને પાછા મૂળ જગ્યાએ આવતા કેટલા .......$min$ નો લઘુતમ સમય લાગશે?View Solution
- 6અક વાહન $4\,km$ નું અંતર $3\,km / h$ ની ઝડપથી અને બીજા $4\,km$ નું અંતર $5\,km / h$ ની ઝડપથી કાપે છે, તો તેની સરેરાશ ઝડપ $..........km/h$View Solution
- 7$150\, m$ લંબાઇ ધરાવતી ટ્રેન $45 \,km/hr$ ની ઝડપથી ગતિ કરે છે,$850 \,m$ લંબાઇ ધરાવતા પુલને પસાર કરવા માટે કેટલા..........$sec$ નો સમય લાગે?View Solution
- 8પ્રારંભિક વેગ અને નિયમિત પ્રવેગ $a$ સાથે એક જ સુરેખ પથ પર ગતિ કરે છે. $t$ અને $( t +1) \sec$ માં કાપેવા અંતરનો સરવાળો $100\,cm$ હોય, તો $t \sec$ પછી તેનો વેગ, $cm /$ s માં.............View Solution
- 9$60 \,km/h$ ઝડપે ગતિ કરતા વાહનને બ્રેક લગાવ્યા બાદ તે $20\, m$ જેટલું અંતર કાપીને ઊભું રહે છે.આ વાહન બમણી ઝડપથી (એટલે કે $120 \,km/h$ થી ) ગતિ કરતું હોય, તો વાહનનું સ્ટોપિંગ ડિસ્ટન્સ ($m$ માં) કેટલું થાય?View Solution
- 10એક ટાવરની ટોચ પરથી ઝડ૫ $u$ સાથે ઉપરથી ફેકવામાં આવે પથ્થર વેગ $4 u$ સાથે જમીન પર પહોંચે છે. ટાવરની ઊંચાઈ ક્ટલી હશે?View Solution
