એક કણ કે જેનો સ્થાન સદીશ $2 \hat{ k }\, m$ છે તેના પર ઉદગમ બિંદુની સાપેક્ષે જ્યારે $3 \hat{ j }\, N$ બળ લાગે ત્યારનું ટોર્ક કેટલું હશે?
NEET 2020, Easy
d
\(\overrightarrow{ F }=3 \hat{j} N , \overrightarrow{ r }=2 \hat{ k }\)
\(\overrightarrow{ F }=3 \hat{j} N , \overrightarrow{ r }=2 \hat{ k }\)
\(\vec{\tau}=\overrightarrow{ r } \times \overrightarrow{ F }=2 \hat{ k } \times 3 \hat{j}=6(\hat{ k } \times \hat{ j })\)
\(=6(-\hat{ i })\)
\(\vec{\tau}=-6 \hat{ i } Nm\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1$M$ દળ અને $R$ ત્રિજયા ધરાવતા નકકર નળાકારને ઢાળ પર મૂકતાં તળિયે તેનો વેગView Solution
- 2$80\ cm$ વિકર્ણ ધરાવતા ચોરસ $ABCD$ ના ખૂણા પર અનુક્રમે $8, 2, 4, 2\ kg$ ના કણ મૂકેલા છે . તો $A$ ખૂણા થી દ્રવ્યમાનકેન્દ્ર નું અંતર ...... $cm$ થાય.View Solution
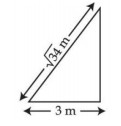
- 3$\sqrt{34} \,m$ લાંબી અને $10 \,kg$ વજન ધરાવતી એક સીડી (નીસરણી) ધર્ષણરહિત દિવાલ પર ટેક્વેલ છે. આકૃતિમાં દર્શાવ્યા પ્રમાણે તેના પગ (નીચેનો છેડો) દિવાલથી $3 \,m$ અંતરે રાખેલ છે. જો $F _{f}$ અને $F _{ w }$ એ અનુક્રમે ભોંયતળિયા અને દિવાલ દ્વારા લાગતું લંબબળ હોય તો ગુણોત્તર $F _{ w } / F _{f}$ ............ થશે.View Solution
$\left(g=10 \,m / s ^{2}\right.$ નો ઉપયોગ કરો.)
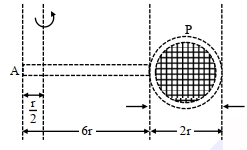
- 4આકૃતિમાં એક બેડમિન્ટન રેકેટના પરિમાણ આપેલા છે. જો બેડમિન્ટનના રેખીય અને વર્તુળાકાર ભાગનું સમાન દળ $(M)$ અને દોરીનું દળ અવગણ્ય હોય તો, હેન્ડલના બિંદુ $A$ થી $\frac{r}{2}$ અંતરે રેકેટના હેન્ડલને લંબ અને રિંગના સમતલમાં રહેલી અક્ષને અનુલક્ષીને જડત્વની ચાકમાત્રા ....... $Mr^2$ જેટલી થાય?View Solution
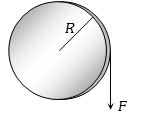
- 5$R$ ત્રિજયા અને $M$ દળ ધરાવતી તકતી તેના કેન્દ્રમાંથી પસાર થતી અને સમતલને લંબ અક્ષને અનુલક્ષીને ચાકગતિ કરી શકે છે.તેના પર સ્પર્શીય બળ $F$ લગાડતાંં સ્પર્શીય પ્રવેગView Solution
- 6$m$ દ્રવ્યમાન $ R$ ત્રિજયાનો એક ઘન ગોળો તેના વ્યાસને અનુલક્ષીને ચાકગતિ કરે છે. સમાન દ્રવ્યમાન અને સમાન ત્રિજયાનો એક નળાકાર પણ તેની ભૌમિતિક અક્ષને અનુલક્ષીને ગોળાની કોણીય ઝડપથી બમણી કોણીય ઝડપથી ગતિ કરે છે. આ બંનેની ચાકગતિ ઊર્જાઓનો ગુણોત્તર $E$ ગોળો$/E$ નળાકાર કેટલો થાય?View Solution
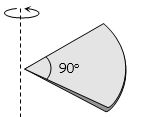
- 7$R$ ત્રિજ્યાની તકતીમાથી તકતીનો $1\over 4 $ ભાગ લીધેલો છે જેનું દળ $M$ છે તેને તેના સમતલને લંબ કેન્દ્રમાથી પસાર થતી અક્ષ ને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય ?View Solution
- 8ઊગમબિંદુથી $\mathop r\limits^ \to = 3\hat i + 2\hat j + 3\hat k$ નો સ્થાન-સદિશ ધરાવતા બિંદુ પર રહેલા કણ ઉપર $\mathop F\limits^ \to = 4\hat i - 3\hat j + 4\hat k\,\,N$ બળ લાગે છે, તો આ કણ પર લાગતું ટૉર્ક .... થાય.View Solution
- 9સમાન તારમાથી બનાવેલ એક સમબાજુ ત્રિકોણ $ ABC$ ના શિરોબિંદુ $A $ પાસે બે સમાન ગોળીઓ રાખેલ છે. ત્રિકોણને $AO$ અક્ષને અનુલક્ષીને ભ્રમણ કરાવવામાં આવે છે. અને પછી આ ગોળીઓને સ્થિર સ્થિતિમાંથી એક સાથે અનુક્રમે $ AB$ અને $ AC$ ની દિશામાં ગતિ કરાવવામાં આવે છે, (જુઓ આકૃતિ) તો ઘર્ષણબળને અવગણતાં, ગોળીઓની અધોદિશામાંની ગતિ દરમિયાન કઇ રાશિઓનું સંરક્ષણ થશે ?View Solution

- 10સમાન દળ અને ત્રિજ્યા ધરાવતાં ચાર વસ્તુઓની જડત્વની ચાકમાત્રા $(M.I.)$ નીચે મુજબ દર્શાવાય છે.View Solution
$I _{1}=$ પાતળી રિંગની તેના વ્યાસને અનુલક્ષીને $M.I.,$
$I _{2}=$ વર્તુળાકાર તકતીની તેના કેન્દ્રમાંથી પસાર થતી અને તકતીને લંબ અક્ષને અનુલક્ષીને $M.I.$
$I_{3}=$ ઘન નળાકારની તેની અક્ષને અનુલક્ષીને $M.I.$ અને
$I _{4}=$ ઘન ગોળાની તેના વ્યાસને અનુલક્ષીને $M.I.$
તો :
