સમાન દળ અને ત્રિજ્યા ધરાવતાં ચાર વસ્તુઓની જડત્વની ચાકમાત્રા $(M.I.)$ નીચે મુજબ દર્શાવાય છે.
$I _{1}=$ પાતળી રિંગની તેના વ્યાસને અનુલક્ષીને $M.I.,$
$I _{2}=$ વર્તુળાકાર તકતીની તેના કેન્દ્રમાંથી પસાર થતી અને તકતીને લંબ અક્ષને અનુલક્ષીને $M.I.$
$I_{3}=$ ઘન નળાકારની તેની અક્ષને અનુલક્ષીને $M.I.$ અને
$I _{4}=$ ઘન ગોળાની તેના વ્યાસને અનુલક્ષીને $M.I.$
તો :
JEE MAIN 2021, Medium
c
Ring \(I _{1}=\frac{ MR ^{2}}{2}\) about diameter
Ring \(I _{1}=\frac{ MR ^{2}}{2}\) about diameter
Disc \(I_{2}=\frac{M R^{2}}{2}\)
Solid cylinder \(I _{3}=\frac{ MR ^{2}}{2}\)
Solid sphere \(I _{4}=\frac{2}{5} MR ^{2}\)
\(I _{1}= I _{2}= I _{3}> I _{4}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
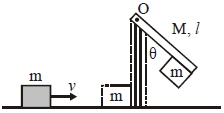
- 1આકૃતિમાં દર્શાવ્યા પ્રમાણે એક $m =1\, kg$ દળનો એક પદાર્થ $v=6\, m / s$ જેટલા વેગથી એક ઘર્ષણરહિત સપાટી પર ગતિ કરીને એક સળિયા સાથે અથડાયને તેની સાથે જોડાય જાય છે. આ સળિયો $O$ બિંદુ સાથે જડેલ છે અને અથડામણના કારણે તે $\theta$ ખૂણો બનાવે છે. જો સળિયાનું દળ $M =2 \,kg $ અને લંબાઈ $l=1\, m $ હોય તો $\theta$ ખૂણાનું મૂલ્ય કેટલું હશે?View Solution
$(\left.g=10 \,m / s ^{2}\right)$
- 2એક પૈડાનો કોણીય પ્રવેગ $3\ rad/s^2$ છે. તેની પ્રારંભિક કોણીય ઝડપ $2\ rad/s $ છે, તો $2\ s$ માં તેણે કેટલું કોણીય સ્થાનાંતર ($rad$ માં) કર્યું હશે ?View Solution
- 3$m$ દળ અને $r$ ત્રિજયાની એક નિયમિત વર્તુળાકાર રીંગ તેના સમતલને લંબ અને તેના કેન્દ્રમાંથી પસાર થતી અક્ષને અનુલક્ષીને $\omega$ કોણીય ઝડપથી ભ્રમણ કરે છે. તેની ગતિઊર્જા કેટલી થાય?View Solution
- 4$l$ લંબાઈના એક હલકા સળિયાનાં બંને છેડે $m_1 $ અને $m_2$ દ્રવ્યમાનના પદાર્થો લગાડેલાં છે. આ સળિયાને લંબ તથા તેના દ્રવ્યમાનકેન્દ્રની અક્ષમાંથી પસાર થતી અક્ષને અનુલક્ષીને તંત્રની જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
- 5View Solutionવર્તૂળાકાર પ્લેટફોર્મની કિનારી પર માણસ ઉભેલો છે. પ્લેટફોર્મના કેન્દ્રમાંથી પસાર થતી અને તેના સમતલને લંબ અક્ષ પર તે અચળ કોણીય ઝડપથી ભ્રમણ કરે છે. જો માણસ ત્રિજ્યા પર ચાલીને અક્ષ તરફ જતો હોય ત્યારે કોણીય વેગ ........ થશે.
- 6એક મીટર સ્ટીકનો તેનાં એક છેડો તળીયા પર રહે તેમ શિરોલંબ રીતે મૂકવામાં આવે છે અને તેને છોડવામાં આવે છે, જ્યારે તેનો બીજો છેડો તળીયા સાથે અથડાય ત્યારે તેની ઝડપ ............... $m / s$ (ધારો કે તળીયા પર રહેલો છેડો લપસી જતો નથી.) $\left(g=9.8 \,m / s ^2\right)$View Solution
- 7$60 \,kg$ દળનો એક માણસ $140 \,kg$ દળ ની એક બોટ પર ઊભો છે કે જે શાંત પાણી માં સ્થિર સ્થિતિમાં છે. તે વ્યક્તિ કાંઠા થી $20\,m$ દૂર છે. તે માણસ કાંઠા તરફ $1.5 \,m / s$ ની અચળ ઝડપે $4 \,s$ સુધી ચાલવાનું શરુ કરે છે. તેનું કાંઠા થી અંતિમ અંતર .............. $m$ હશે.View Solution
- 8એક વજનદાર નક્કર ગોળાને એક ખરબચડી સમક્ષિતિજ સપાટી ઉપર ગબડ્યા વગર પ્રારંભિક વેગ $u$ સાથે ફેકવાામાં આવે છે. જ્યારે તે શુદ્ધ રોલિંગ (ગબડતી) ગતિ શરૂ કરે ત્યારે તેની ઝડપ શું થશે?View Solution
- 9View Solutionપૃથ્વીની અંદરથી વિવિધ પ્રકારના ખનીજોને ખોદવામાં આવે છે, અને બહુમાળીય ઈમારતો બાંધવામાં આવે છે. આ પ્રવૃતિને કારણો સૈદ્ધાંતિક રીતે,
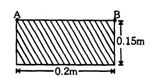
- 10$20\ kg$ દળની લંબચોરસ પ્લેટને આકૃતિમાં દર્શાવ્યા પ્રમાણે બિંદુ $ A$ અને $ B$ પરથી લટકાવેલી છે. જો $ B$ પિનને અચાનક દૂર કરવામાં આવે તો, પ્લેટનો કોણીય પ્રવેગ $(in\ rad/ sec^2)$ શોધો ?View Solution