એક $L =400 \;mH$ નો ઈન્ડકટર, $R _{1}=2 \;\Omega$ નો અવરોધ, અને $R _{2}=2 \;\Omega$ નો બીજો અવરોધ એ $12 \;V$ ના $emf$ વાળી બેટરી સાથે જોડેલા છે. બેટરીનો આંતરિક અવરોધ અવગણ્ય છે. $t=0$ સમયે સ્વીચ $s$ બંધ છે. $L$ આગળ વિદ્યુતસ્થિતિમાનમાં ધટાડો કેટલો થશે?
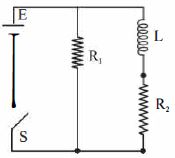

AIEEE 2009, Diffcult
d
Growth in current in \(L R_{2}\) branch when switch is closed is given by
Growth in current in \(L R_{2}\) branch when switch is closed is given by
\(i=\frac{E}{R_{2}}\left[1-e^{-R_{2} t / L}\right] \Rightarrow \frac{d i}{d t}=\frac{E}{R_{2}} \cdot \frac{R_{2}}{L} e^{-R_{2} t / L}=\frac{E}{L} e^{-\frac{R_{2} t}{L}}\)
Hence, potential drop across
\(\mathrm{L}=\left(\frac{E}{L} e^{-R_{2} t / L}\right) L=E e^{-R_{2} t / L}=12 e^{-\frac{2 t}{400 \times 10^{-3}}}\)
\(=12 \mathrm{e}^{-5 \mathrm{t}}\, \mathrm{V}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1View Solutionડાયનેમો કયાં સિધ્દ્વાંત પર કાર્ય કરે છે.
- 2એક લાંબા સોલેનોઇડના આંટાની સંખ્યા $1000 $ છે. જયારે તેમાંથી $4\;A$ નો પ્રવાહ વહેતો હોય, ત્યારે સોલેનોઇડના દરેક આંટા સાથે સંકળાયેલ ફ્લકસ $4 \times10^{-3} \;Wb$ છે. આ સોલેનોઇડનું આત્મપ્રેરકત્વ ....... $H$ હશે?View Solution
- 3એક વિદ્યુત અવરોધ કોપરના તારના $100$ આાંટાને લાકડાની નળાકાર કોર કે જેનું આડછેદનું ક્ષેત્રફળ $24\,cm ^2$ છે તેને વીટાળવામાં આવે છે. તારના બંને છેડાને અવરોધ સાથે જોડવામાં આવે છે પરીપથનો કુલ અવરોધ $12\,\Omega$ છે. જો કોઈ ઉપર અક્ષની દિશામાં $1.5\,T$ નું અને $1.5\,T$ નું તેની વિરુદ્ધ દિશામાં બાહ્ય રીતે સમાન ચુંબકીય બળ લગાડવામાં આવે, તો પરિપથમાંથી તે બિંદુ પાસેથી પસાર થતા વીજભારમાં થતો ફેરફાર ............ $mC$ હશે.View Solution
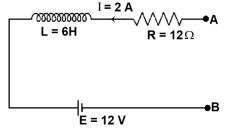
- 4આપેલ આકૃતિ મુજબ, જો $\frac{ dI }{ dt }=-1\,A / s$ હોય, તો આ ક્ષણે $V _{ AB }$ નું મૂલ્ય $...........\,v$ હશે.View Solution
- 5$0.01 m^2$ ક્ષેત્રફળ ધરાવતી લૂપ $2\, T$ ચુંબકીયક્ષેત્રને લંબ છે,$10^{-3} seconds$ સમયમાં ચુંબકીયક્ષેત્ર $1\,T$ થાય છે,જો લૂપનો અવરોધ $0.0.1\,Ω$ હોય,તો લૂપમાં કેટલા .......$J$ ઉષ્મા ઉત્પન્ન થાય?View Solution
- 6View Solutionવિદ્યુતચુંબકીય પ્રેરણના સિધ્દ્વાંત પર કાર્ય કરતું સાધન નીચેનામાંથી કયું છે?
- 7View Solutionમોટર સ્ટાર્ટર એે
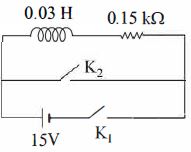
- 8નીચે દર્શાવેલ પરિપથમાં એક ઇન્ડકટર $(L=0.03H)$ અને અવરોધ $(R=0.15$ $K\Omega)$ એક $15$ $V$ $emf$ ધરાવતી બેટરી સાથે શ્રેણીમાં જોડેલા છે.કળ $K_1$ ને ઘણા લાંબા સમય સુધી બંધ રાખવામાં આવે છે.પછી, $t=0$ સમયે કળ ને ખોલવામાં $(open)$ આવે છે અને તે જ સમયે કળ $K_2$ ને બંધ $(close)$ કરવામાં આવે છે.$t= 1$ $ms$ ને અંતે પરિપથમાં વહેતો પ્રવાહ .......... $mA$ હશે. (${e^5} \cong 150)$View Solution
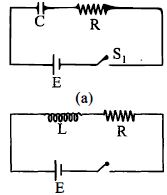
- 9આપેલ પરિપથ $(a)$ અને $(b)$ માટે $t = 0$ સમયે કળ $S_1$ અને $S_2$ ને બંધ કરેલ છે અને તેને લાંબા સમય સુધી બંધ રાખવામા આવે છે. બે પરિપથમાં $t \ge 0$ માટે વહેતા પ્રવાહનો સમય સાથેનો સંબંધ નીચે પૈકી કયો આલેખ દર્શાવે છે?View Solution
- 10$2.0\,A$ પ્રવાહધારીત પરિપથમાં પસાર થતું ફલક્સ $0.8\,Weber$ છે.તે પ્રવાહ $0.1\,s$ માં $1.5\,A$ કરતાં ઉદભવતું $e.m.f.$......$V$View Solution
