એક લિસી સપાટીવાળો $A$ ગોળો એક ઘર્ષણરહિત સમક્ષિતિજ પર કોણીય વેગ $\omega$ અને તેનું દ્રવ્યમાન કેન્દ્ર $v $ વેગ થી ગતિ કરે છે. તે પોતાના જેવા જ બીજા સ્થિર ગોળા $B$ સાથે સ્થિતિસ્થાપક સંઘાત અનુભવે છે. જો સંઘાત પછી તેના કોણીય વેગ અનુક્રમે $\omega_A$ અને $\omega_B$ છે બધી જગ્યાએ ઘર્ષણ અવગણઈએ તો નીચેમાંથી શું સાચું છે ?
IIT 1999, Medium
c
As the spheres are smooth there will be no friction (no torque) and therefore there will be no transfer of angular momentum. Thus \(\mathrm{A}\), after collision will remain with its intial angular momentum \(i . e ., \omega_{A}=\omega\)
As the spheres are smooth there will be no friction (no torque) and therefore there will be no transfer of angular momentum. Thus \(\mathrm{A}\), after collision will remain with its intial angular momentum \(i . e ., \omega_{A}=\omega\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1દરેક $M$ દળ ધરાવતા ત્રણ એક સમાન ગોળાઓને કાટકોણ ત્રિકોણના ખૂણાઓ (શિરોબિંદુ) પર મૂકવામાં આવ્યા છે. કાટકોણ ત્રિકોણની એકબીજાને લંબ બાજુ $3\,m$ ની છે. આ બે એકબીજાને લંબ બાજુનાં અંતઃ છેદને ઉગમ બિંદુ તરીકે લઈ દ્રવ્યમાન કેન્દ્રના સ્થાન સદિશના માનાંક $\sqrt{x} m$ છે, તો $x=........$ થશે.View Solution
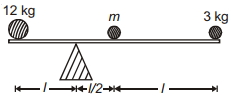
- 2તંત્રના સંતુલન માટે, $m$ દળનું મૂલ્ય .............. $kg$ થાય?View Solution
- 3એક નિયમિત ઘનતાવાળી તકતી $10$ પરિભ્રમણ પ્રતિ સેકન્ડ કરે છે. તેની ઉપર ટૉર્ક લગાડતાં તેમાં $5\ rad s^{-2}$ નો કોણીય પ્રવેગ ઉત્પન્ન થાય છે.$2\ s $ બાદ તેનો કોણીય વેગ ......$ rad s^{-1}$ અને $2\ s$ માં તકતીએ કરેલાં પરિભ્રમણ ...... થાય.View Solution
- 4એક પૈડાને $1000\ N-m$ નું ટોર્ક આપતા તે તેના કેન્દ્રમાંથી પસાર થતા અક્ષની આસપાસ $200\ kg-m^2$ જડત્વની ચાકમાત્રા સાથે ફરે છે. તો $3 $ સેકન્ડ પછી પૈડાનો કોણીય વેગ $=$ ......... $\ rad/s$View Solution
- 5View Solutionસમાન દળ અને સમાન દ્રવ્યમાંથી બનાવેલ ઘન ગોળો, તકતી અને ઘન નળાકારને ઢળતા સમતલ પર મૂકીને (સ્થિર સ્થિતિમાં) ગબડાવવામાં આવે, તો......
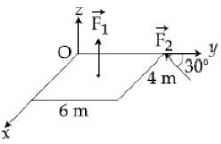
- 6આકૃતિમાં બતાવ્યા પ્રમાણે એક ચોસલા પર સમાન માન $F$ ના બે બળો ${\vec F_1}$ અને ${\vec F_2}$ લગાડવામાં આવે છે. બિંદુ $(2\vec i + 3\vec j)$ આગળ બળ ${\vec F_2}\,XY- $ સમતલમાં છે જ્યારે ${\vec F_1} \,Z- $ દિશામાં લાગે છે. $O$ બિંદુને સાપેક્ષે આ બળોની ચકમાત્રા કેટલી થાય?View Solution
- 7એક ઘન સમાન શંકુના શિરોબિંદુથી દ્રવ્યમાન કેન્દ્રથી અંતર $z_0$ છે.જો તેના આધારની ત્રિજયા $R$ અને ઊંચાઇ $h$ હોય,તો $z_0$ _________ બરાબર થશે.View Solution
- 8$m$ દળનો એક પત્થર કોઈ દોરીના છેડે બાંધીને એક સમક્ષિતિજ ઘર્ષણરહિત ટેબલ પર વર્તુળાકારે ફેરવવામાં આવે છે. પત્થરનું કોણીય વેગમાન વર્તુળના કેન્દ્રને અનુલક્ષીને અચળ રહે તેમ દોરીની લંબાઈ ધીમે ધીમે ઘટાડવામાં આવે છે. દોરીનું તણાવ $T\, = Ar^n$ (જ્યાં $A$ એ અચળાંક છે) દ્વારા આપેલ છે, એ વર્તુળની તત્કાલિન ત્રિજ્યા છે. તો $n$ ની કિંમત શું હશે?View Solution
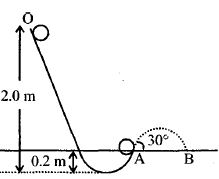
- 9એક ટેનિસ બોલ (પોલું ગોળીય કવચ) ટેકરી પર $O$ થી શરૂ કરીને નીચે તરફ દડે છે. બિંદુ $A$ પાસે દડો હવામાં ઊછળવાની શરૂઆત સમક્ષિતિજ સાથે $30^o$ ના ખૂણેથી કરે છે. $B$ પાસે દડો જમીન પર પહોચે છે. તો અંતર $AB$ ની કિંમત ......... $m$ થાય. ( દળ $m$ અને ત્રિજ્યા $R$ વાળા પોલા ગોળીય કવચની તેના વ્યાસને અનુલક્ષીને જડત્વની ચાકમાત્રા $= \frac {2}{3}\,mR^2$)View Solution
- 10$R$ ત્રિજયાવાળો ઘન ગોળો ધર્ષણરહિત સમક્ષિતિજ સપાટી પર પડેલ છે. $F$ સમક્ષિતિજ બળ નીચેના બિંદુથી $h$ ઊંચાઇ પર લગાવતા દ્રવ્યમાનકેન્દ્રનો મહત્તમ પ્રવેગ મેળવવા માટે નીચે પૈકી શું સાચું થાય?View Solution
