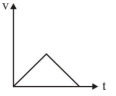
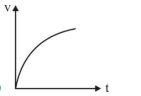
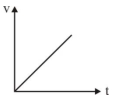
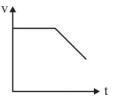
\(\mathrm{mg}-\mathrm{F}_{\mathrm{B}}-\mathrm{F}_{\mathrm{v}}=\mathrm{ma}\)
\(\left(\rho \frac{4}{3} \pi \mathrm{r}^3\right) \mathrm{g}-\left(\rho_{\mathrm{L}} \frac{4}{3} \pi \mathrm{r}^3\right) \mathrm{g}-6 \pi \eta \mathrm{r}=\mathrm{m} \frac{\mathrm{dv}}{\mathrm{dt}}\)
\(\text { Let } \frac{4}{3 \mathrm{~m}} \pi \mathrm{R}^3 \mathrm{~g}\left(\rho-\rho_{\mathrm{L}}\right)=\mathrm{K}_1 \text { and } \frac{6 \pi \eta \mathrm{r}}{\mathrm{m}}=\mathrm{K}_2\)
\(\frac{\mathrm{dv}}{\mathrm{dt}}=\mathrm{K}_1-\mathrm{K}_2 \mathrm{v}\)
\(\int_0^{\mathrm{v}} \frac{\mathrm{dv}}{\mathrm{K}_1-\mathrm{K}_2 \mathrm{v}}=\int_0^{\mathrm{t}} \mathrm{dt}\)
\(-\frac{1}{\mathrm{~K}_2} \ln \left[\mathrm{K}_1-\mathrm{K}_2 \mathrm{v}\right]_0^{\mathrm{v}}=\mathrm{t}\)
\(\ln \left(\frac{\mathrm{K}_1-\mathrm{K}_2 \mathrm{v}}{\mathrm{K}_1}\right)=-\mathrm{K}_2 \mathrm{t}\)
\(\mathrm{K}_1-\mathrm{K}_2 \mathrm{v}=\mathrm{K}_1 \mathrm{e}^{-\mathrm{K}_2 \mathrm{t}} \)
\(\mathrm{v}=\frac{\mathrm{K}_1}{\mathrm{~K}_2}\left[1-\mathrm{e}^{-\mathrm{K}_2 \mathrm{t}}\right]\)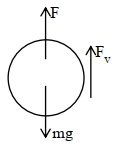
Download our appand get started for free
Similar Questions
- 1નીચે બે વિધાનો આપેલા છેView Solution
વિધાન $I:$ પાણીના સંગ્રહ સ્થાનમાં સમાન સ્તર પર બધા જ બિદુંએ દબાણ સમાન હોય છે.
વિધાન $II:$ બંધિત પાણી પર લગાડેલું દબાણ બધી જ દિશાઓમાં એક સરખુ પ્રસરણ પામે છે.
ઉપર્યુક્ત વિધાનોના સંદર્ભમાં, નીચે આપેલા વિકલ્પોમાંથી સાચો ઉત્તર પસંદ કરો.
- 2$1$ મી પાણી ભરેલા પાત્રમાં તળીયેથી $0.25$ મી અંતરે છિદ્ર પાડતાં તેની અવધિ ...... (સેમી માં)View Solution
- 3ઊંચી એડીના બુટ પહેરતી $50\, kg$ ની એક છોકરી એક એડી પર સંતુલન જાળવે છે. બુટની એડીનો વ્યાસ $1.0\, cm$ છે. એડી વડે સમક્ષિતિજ તળિયા પર કેટલું દબાણ લાગે ?View Solution
- 4એક ખુલ્લા ગ્લાસની નળીને પારામાં એવી રીતે ડૂબાડવામાં આવે છે કે જેથી $8$ $cm$ લંબાઇની નળી પારાની સપાટીથી ઉપર રહે છે.નળીના ખુલ્લા છેડાને બંધ કરી સીલ કરવામાં આવે છે.નળાને ઊર્ધ્વ દિશામાં $46$ $cm$ રહેલ જેટલી વધારે ઊંચી લઇ જવામાં આવે છે,તો હવે નળીની અંદર રહેલ હવાના સ્તંભની લંબાઇ ........ $cm$ હશે.( વાતાવરણનું દબાણ $=$ $Hg$ ના $76$ $cm$ )View Solution
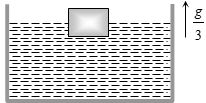
- 5સમઘન બ્લોકનું અડધું કદ ડુબેલું છે,પાત્રને $g/3$ પ્રવેગથી ઉપર તરફ ગતિ કરાવવાથી ડુબેલું નવું કદ કેટલું થાય?View Solution
- 6$47.6\, m$ ઊંડાઇ ધરાવતું તળાવમાં તળિયે $50\, cm^{3}$ કદ ધરાવતો પરપોટો સપાટી પર આવે ત્યારે તેનું નવું કદ ....... $cm^{3}$ થાય. (atmospheric pressure $= 70\, cm$ of Hg and density of $Hg = 13.6 g/cm^{3}$)View Solution
- 7$a$ ત્રિજ્યાની કેશનળીમાંથી પાણીનું ધારી રેખીય રીતે વહન થઈ રહ્યું છે. દબાણનો તફાવત $P$ છે અને વહનનનો દર $Q$ છે. જો ત્રિજ્યા એ $\frac{a}{4}$ જેટલી ઘટી જાય અને દબાણ $4 P$ જેટલું વધી જાય તો વહનનો દર દેટલો થશે ?View Solution
- 8$10 \,mm$ કે તેથી વધુ મરક્યુરીનું લેવલ ૫ડતું તે શું દર્શાવે છે ?View Solution
- 9પર્વતના તળિયે અને ઉપર બેરોમીટરમાં મરકયુરીની ઊંચાઇ $75\, cm $ અને $50\, cm$ છે.જો મરકયુરીની અને હવાની ઘનતાનો ગુણોત્તર $10^4$ છે,તો પર્વતની ઊંચાઇ કેટલી હશે?View Solution
- 10View Solutionદબાણ માટે ખોટું નિવેદન પસંદ કરો.