એક નકકર નળાકાર કે જેની લંબાઈ $L$ અને ત્રીજ્યા $r$ છે તો બાજુની લંબાઈ $a$ ના ઘન જેટલો ગરમ કરવામાં આવે છે જો બન્ને સરખા પદાર્થ, કદ અને સરખા તાપમાને ઠંડા પાડવામાં આવે છે તો રેડીયેશનનો ગુણોત્તર કેટલો થશે? (નળાકારની સમતલ સપાટીનું રેડીયેશન ઉત્સર્જનને અવગણો.)
Medium
a
(a)
(a)
\(\because\) Both have same volume
\(\therefore a^3=\pi r^2 L \quad \dots (1)\)
Amount of radiation \(\propto\) Surface area [ \(\because\) Temperature, material are same for both]
[ \(\because\) Temperature, material are same for both]
\(\frac{\text { Radiation cylinder }}{\text { Radiation cube }}=\frac{2 \pi r L}{6 a^2}=\frac{2 \pi r L \cdot a}{6 a^3}\)
using equation \((1)\)
We get
\(\frac{R_{\text {cylinder }}}{R_{\text {cube }}}=\frac{a}{3 r}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1બે સમાન પદાર્થોના તાપમાન $ {727^o}C $ અને $ {327^o}C $ છે,તો ઉત્સર્જન ઊર્જાનો ગુણોત્તર કેટલો થાય?View Solution
- 2જો પદાર્થની સપાટી નો શોષક ગુણાંક અને પરાવર્તક ગુણાંક અનુક્રમે $0.4$ અને $0.6$ ત્યારે.....View Solution
- 3$R$ ત્રિજ્યા અને $M$ દળ ધરાવતા કાળા કલરના ગોળા ની અંદર બખોલ છે જેની અંદર શૂન્યાવકાશ છે.બખોલની દીવાલનું તાપમાન $T_0$ જાળવી રાખવામા આવેલ છે. ગોળાનું શરૂઆતનું તાપમાન $3T_0$ છે.જો $T$ તાપમાને રહેલ ગોળાના દ્રવ્ય માટે એકમ દળ દીઠ વિશિષ્ટ ઉષ્મા $\alpha T^3$ મુજબ ફરે છે જ્યાં $\alpha $ અચળાંક છે.તો ગોળાનું તાપમાન $2T_0$ થતાં કેટલો સમય લાગશે?View Solution
- 4એક કાળા પદાર્થનું તાપમાન $727^o C$ છે. તેમાંથી ઉત્સર્જાતી ઊર્જાનો દર કોના સમપ્રમાણમાં હશે?View Solution
- 5View Solutionસંપૂર્ણ સૂર્યગ્રહણ દરમિયાન ફોનહોફર રેખાઓ સ્પષ્ટ દેખાય છે કારણ કે.....
- 6જયારે સંપૂર્ણ કાળા પદાર્થનું તાપમાન વધારવામાં આવે છે ત્યારે $\lambda_m$ નું મૂલ્ય $0.26 \mu_m$ થી $0.13 \mu_m$ નો ફેરફાર અનુભવે છે તો આ તાપમાનને અનુલક્ષિને તેની ઉત્સર્જન પાવરનો ગુણોત્તર ……View Solution
- 7એક તળાવના લંબચોરસ તળિયાની સપાટીનું ક્ષેત્રફળ $A$ છે, જેમાં પાણી (ઘનતા $=\rho,$ વિશિષ્ટ ઉષ્મા $=s$) ભરેલું છે જેની બહારની હવાનું તાપમાન $-26^{\circ} \mathrm{C}$ જેટલું અચળ છે. તળાવમાં પાણી પર બરફના સ્તરની જાડાઈ કોઈ એક સમયે $x$ છે.View Solution
બરફની ઉષ્માવાહકતા ${K}$ અને ગલનગુપ્તઉષ્મા $L$ લેવામાં આવે, તો કોઈ ક્ષણે બરફના સ્તરમાં થતાં વધારાનો દર શેના વડે આપવામાં આવે?
- 8View Solutionમાણસના શરીર દ્વારા ઉત્સર્જન પામતા વિકિરણને ધ્યાનમાં લો. તેના માટે નીચેનામાથી શું સાચું છે?
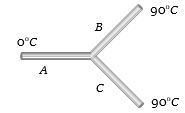
- 9ત્રણ સમાન દ્રવ્ય, સમાન લંબાઈ અને સમાન આડછેદ વાળા સળિયાને જોડીને આકૃતિમાં દર્શાવ્યા પ્રમાણે જોડેલા છે.ડાબી અને જમણી બાજુને અનુક્રમે ${0^o}C$ અને ${90^o}C$ તાપમાને રાખેલ છે. તો ત્રણેય સલિયાના જંકશન પાસેનું તાપમાન ....... $^oC$ થાય?View Solution
- 10પદાર્થનું તાપમાન $ {7^o}C $ થી વધીને $ {287^o}C $ થાય છે,તો ઉત્સર્જન ઊર્જા કેટલા ગણી વધે?View Solution
