\(\,{l}\,\, = \,\,(4.00\,\, \pm \,\,0.01\,\,)\,cm\) \(\therefore l\) ના માપનમાં આંશિક ત્રુટિ \( = \,\,\,\frac{{\Delta {l}}}{{l}}\, = \,\frac{{0.01}}{{4.0}}\, = \,0.0025\)
\(r\,\, = \,\,(0.250\,\, \pm \,\,0.001\,)\,\,cm\,\,\) \(\therefore R\) ના માપનમાં આંશિક ત્રુટિ \( = \,\,\,\,\frac{{\Delta r}}{r}\, = \,\frac{{0.001}}{{0.250}}\, = \,0.004\)
\(m\,\, = \,\,(6.25\,\, \pm \,\,0.01)\,\,g\,\,\,\,\) \(\therefore M\) ના માપનમાં આંશિક ત્રુટિ \( = \,\,\,\,\frac{{\Delta m}}{m} = \frac{{0.01}}{{6.25}}\, = \,0.0016\)
ઘનતા = દળ /કદ \( = \,\,\frac{m}{{\pi {r^2}{l}}}\,\) પરથી દ્રાવ્યની ઘનતામાં આંશિક ત્રુટિ \( = \,\,\frac{{\Delta \rho }}{\rho }\, = \,\frac{{\Delta m}}{m}\, + \,\frac{{2\Delta r}}{r} = \frac{{\Delta {l}}}{{l}}\)
પ્રતિશત ત્રુટિ \(\, = \,\frac{{\Delta \rho }}{\rho } \times \,100\,\% \) \( = \left( {\frac{{\Delta m}}{m} \times \,100} \right)\% + \) \(2\left( {\frac{{\Delta r}}{r} \times 100} \right)\% + \left( {\frac{{\Delta {l}}}{{l}} \times \,100} \right)\% \)
\( = \,(0.0025\, \times \,100)\,\% \,\, + \,\,2(0.004\, \times \,100)\% \,\, + \,\,(0.0016\, \times 100)\,\% \)
\(\, = \,0.25\% \, + \,0.8\% + \,0.16\,\% = \,1.21\% \)
Download our appand get started for free
Similar Questions
- 1View Solutionપ્રતિશત ત્રુટીનો એકમ શું થાય?
- 2વિધાન $A:$ જો વર્તુળાકાર સ્કેલ પરના પાંચ પૂર્ણ પરિભ્રમણ માટે સ્ક્રૂ ગેજના મુખ્ય સ્કેલ પર કપાયેલ અંતર $5\, {mm}$ અને વર્તુળાકાર સ્કેલ પર કુલ કાપા $50$ હોય તો તેની લઘુત્તમ માપશક્તિ $0.001\, {cm}$ છે.View Solution
કારણ $R:$ લઘુત્તમ માપશક્તિ = પિચ/ વર્તુળાકાર સ્કેલ પરના કુલ કાપા
ઉપરોક્ત વિધાનોના સંદર્ભમાં, નીચે આપેલા વિકલ્પો પૈકી સૌથી યોગ્ય જવાબ પસંદ કરો.
- 3જો $a, b, c$ ના પરિમાણમાં જો $A, B$ અને $C$ એ પ્રતિશત ત્રુટિ હોય તો $ABC$ ની અંદાજીત ત્રુટિ કેટલી હશે ?View Solution
- 4માપિત મૂલ્ય $4.700 \,m$ માં સાર્થક અંકોની સંખ્યા એ .............. $m$ મૂલ્ય જેટલી જ છે.View Solution
- 5એક બીકરમાં $\rho \ kg / m^3$ ઘનતા, વિશિષ્ટ ઉષ્મા $S J / \ kg^\circ C$ અને શ્યાનતા $\eta $ વાળું પ્રવાહી ભરેલ છે, બીકર $h$ ઊંચાઈ સુધી ભરેલ છે. બીકરને ગરમ પ્લેટ પર મૂકતા તેમાં સંવહન દ્વારા એકમ ક્ષેત્રફળ દીઠ ઉષ્મા પ્રસરણ દર $(Q/A)$ ના અનુમાપન માટે એક વિદ્યાર્થી ધારે છે કે તે $\eta \;\left( {\frac{{S\Delta \theta }}{h}} \right)$ અને $\left( {\frac{1}{{\rho g}}} \right)$ પર આધારિત છે, જ્યા $\Delta \theta (^\circ C$ માં$)$ એ ઉપરના અને નીચેના ભાગના તાપમાનનો તફાવત છે. આ પરિસ્થિતિમાં $(Q / A)$ માટે નીચેનામાથી કયું સાચું છે$?$View Solution
- 6વિદ્યુત પરિપથમાં ઉત્પન્ન થતી ઉષ્માનો જથ્થો વિદ્યુત પ્રવાહ $(I)$, અવરોધ $(R)$ અને સમય $(t)$ પર આધાર રાખે છે. જો ઉપરની ભૌતિક રાશિઓના અનુક્રમે $2\%\,, 1\%$ અને $1\%$ ની ત્રુટિઓ મળે, તો ઉત્પન્ન થતી કુલ ઉષ્મામાં મહત્તમ શક્ય ત્રુટિ કેટલા .............. $\%$ હશે ?View Solution
- 7પારિમાણીક સામ્યતા (સમાનતા)ના સિદ્ધાંત અનુસાર નીચેનામાંથી કયું સાયું છે તે દર્શાવો.જ્યાં $T$ એ આવર્તકાળ, $G$ એ ગુરુત્વકર્ષી અયળાંક, $M$ દળ અન $r$ એ કક્ષાની ત્રિજ્યા છે.View Solution
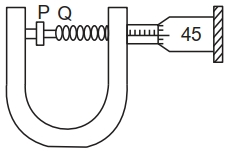
- 8સ્ક્રુગેજની મદદથી તારનો વ્યાસ માપવાના એક પ્રયોગમાં નીચે મુજબના અવલોકનો મળે છે.View Solution
$(A)$ એક પૂર્ણ પરિભ્રમણ માટે સ્ક્રુ મુખ્ય સ્કેલ ઉપર $0.5\,mm$ ખસે છે.
$(B)$ વર્તુળાકાર સ્કેલ પર કુલ $50$ કાપા છે.
$(C)$ મુખ્ય સ્કેલ પરનું અવલોકન $2.5\,mm$ છે.
$(D)$ વર્તુળાકાર સ્કેલ પરનો $45$ મો કાપો પીચ-રેખા પર આવે છે.
$(E)$ સાધનને $0.03\,mm$ જેટલી ઋણ ત્રુટી છે.
તો તારનો વ્યાસ $............\;mm$ થશે.
- 9પતરા પર લાગતા બળ અને તેની બાજુઓની લંબાઈની મદદથી ચોરસ પતરા પરનું દબાણ માપેવામાં આવે છે, જો બળ અને લંબાઈના માપનમાં મહત્તમ ત્રુટિ અનુક્રમે $4\%$ અને $2\%$ હોય તો દબાણના માપનમાં મહત્તમ ત્રુટિ ........ $\%$ હશે .View Solution
- 10બે રાશિના મૂલ્યો સાધનથી ચોકચાઈ પૂર્વક માપતા $A = 2.5\,m{s^{ - 1}} \pm 0.5\,m{s^{ - 1}}$, $B = 0.10\,s \pm 0.01\,s$ મળે છે. તો $AB$ નું માપન કેટલું થાય?View Solution
