એક પૈડું સ્થિર સ્થિતિમાંથી $6\ sec$ માં $540\ rpm $ ની કોણીય ઝડપ પ્રાપ્ત કરે,તો તેનો કોણીય પ્રવેગ કેટલો થાય?
Easy
Download our app for free and get started
a
\(\mathrm{n}=\frac{540}{60}=9 \mathrm{r.p.s.}, \omega=2 \pi \mathrm{n}=18 \pi \mathrm{rad} / \mathrm{s}\)
\(\mathrm{n}=\frac{540}{60}=9 \mathrm{r.p.s.}, \omega=2 \pi \mathrm{n}=18 \pi \mathrm{rad} / \mathrm{s}\)
Angular acceleration
\(=\frac{\text { Gain in angular velocity }}{\text { time }}=\frac{18 \pi}{6}=3 \pi \mathrm{rad} \mathrm{s}^{-2}\)
Download our appand get started for free
Experience the future of education. Simply download our apps or reach out to us for more information. Let's shape the future of learning together!No signup needed.*
Similar Questions
- 1એક હળવા સળિયાના છેડે $1.5\, {kg}$ દળ અને $50\, {cm}$ ત્રિજયાના બે સમાન ગોળા જોડેલા છે. બંને ગોળાના કેન્દ્ર વચ્ચેનું અંતર $5\, {m}$ છે. તો આ સળિયાના મધ્યબિંદુમાંથી પસાર થતી અને સળિયાને લંબ એક્ષાને અનુલક્ષીને જડત્વની ચાકમાત્રા (${kgm}^{2}$ માં)કેટલી થાય?View Solution
- 2$200 g$ અને $500 g$ દળવાળા કણો $10\,\hat i\,\,m/s\,$ અને $3\,\hat i + 5\,\hat j\,\,m/s $ અનુક્રમે ના વેગથી ગતિ કરે છે, તો કણોથી બનતા તંત્રના દ્રવ્યમાન કેન્દ્ર નો વેગ .................. થાય.View Solution
- 3View Solutionફલાય વ્હીલને એવી રીતે બનાવવામાં આવે છે જેથી તેનું સંપૂર્ણ દળ તેની રીમ પર સંકેન્દ્રિત થયેલું હોય છે, કારણ કે......
- 4$r $ ત્રિજ્યાવાળા સમાન પ્રકારના ત્રણ દડાઓ એકબીજાને અડે તેમ સમક્ષિતિજ સપાટી પર મૂકેલા છે. આ દડા એવી રીતે ગોઠવેલા છે, જેથી તેમના દ્રવ્યમાન-કેન્દ્રને જોડતા તેઓ સમબાજુ ત્રિકોણ બનાવે. આ તંત્રનું દ્રવ્યમાન-કેન્દ્ર ........ હશે.View Solution
- 5બળ $\mathop {\text{F}}\limits^ \to \,\, = \,\,2\hat i\,\, + \;\,\hat j\,\, + \;4\hat k\,$ અને $ \mathop r\limits^ \to \,\, = \,\,7\hat i\,\, + \;3\hat j\,\, + \;\,\hat k\,$ બિંદુ આગળ ટોર્ક ...... હોય.View Solution
- 6ચાકગતિ કરતું ટેબલ $ 10\ s$ એક ભ્રમણ પૂર્ણ કરે છે. અને તેની જડત્વની ચાકમાત્રા $100$ $kg - m^2$ છે. $50\ kg $ દળનો માણસ ભ્રમણ કરતાં ટેબલના કેન્દ્ર પર ઊભો છે. જો માણસ કેન્દ્રથી $2\ m$ દૂર જાય તો ટેબલનો કોણીય વેગ $rad/sec$ માં કેટલો થશે ?View Solution
- 7View Solutionવર્તૂળાકાર પ્લેટફોર્મની કિનારી પર માણસ ઉભેલો છે. પ્લેટફોર્મના કેન્દ્રમાંથી પસાર થતી અને તેના સમતલને લંબ અક્ષ પર તે અચળ કોણીય ઝડપથી ભ્રમણ કરે છે. જો માણસ ત્રિજ્યા પર ચાલીને અક્ષ તરફ જતો હોય ત્યારે કોણીય વેગ ........ થશે.
- 8$M$ દળ અને $R$ ત્રિજ્યા ધરાવતા વર્તુળાકાર તારની વ્યાસને અનુલક્ષીને જડત્વની ચાકમાત્રા કેટલી થાય?View Solution
- 9પ્રત્યેકનું દળ $1 \mathrm{~kg}$ હોય તેવા ચાર કણોને $2 \mathrm{~m}$ બાજુ ધરાવતા ચોરસના ચાર ખૂણા પર મૂકેલા છે. તેના એક શિરોબિંદુમાંથી પસાર થતી અને સમતલને લંબ અક્ષને અનુલક્ષીને તંત્રની જડત્વની ચાક્માત્રા______$\mathrm{kg} \mathrm{m}^2$છે.View Solution
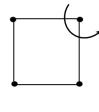
- 10આકૃતિમાં દર્શાવ્યા પ્રમાણે $a$ બાજુવાળો સમઘન બોક્સ એક રફ સપાટી પર પડેલ છે તેને ખસેડવા માટે તેના દ્રવ્યમાનથી $b$ ઊંચાઈ ઓછામાં ઓછા $F$ બળની જરૂર પડે છે.જો સપાટીનો ઘર્ષણાંક $\mu=0.4$ હોય તો બોક્સને ગબડયા વગર ખસેડવા માટે $100 \times \frac{b}{a}$ નું મહત્તમ મૂલ્ય કેટલું હોવું જોઈએ?View Solution
